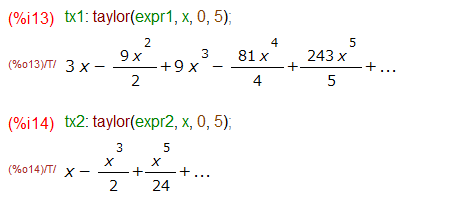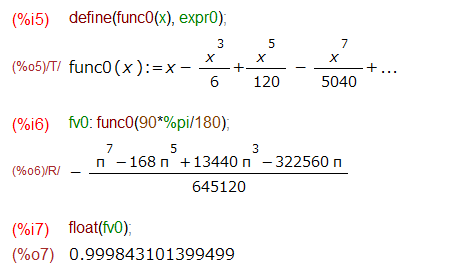世間は連休というのに、唐突にマクローリン展開つかって極限を求めることになりました。ということで(どういうことだ)線形代数の練習は1回お休みしてマクローリン展開です。そして極限。何も言わないでもMaxima様は内部でマクローリン展開使っているみたいです。そこをあえて刻んでみると。これまたMaxima様にお願い。
※「忘却の微分方程式」投稿順 index はこちら
微分さえできれば後は機械的に求められるテイラー展開はMaxima様にとってはなんのこともありません。以下の関数で求まってしまうのでございます。
taylor(expr,x,a,n)
さらにいえば、上記の関数表記で a=0 のときこそが、マクローリン展開となります。
マクローリン展開、近似値計算
例題の定番中の定番 sin関数をマクローリン展開してみたいと思います。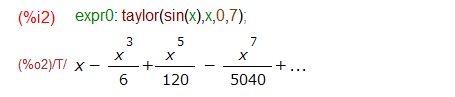
無限につづく多項式が現れて参りました。級数展開できたぞなもし。上記はn=7としたので表示されているのは7乗の項までであるようです。しかしちょっと気になるところがあります。出力ラベルの後です
(%o2)/T/
(%o2)は後で出力結果を再利用するための出力ラベルですが、その後に見かけない/T/とかかれております。なんじゃらほい? 調べたら以下の日本語ページに説明が書かれていました。
Maxima様は多項式を表現するのに2つの異なる形式を使っているようなのです。
-
- 一般形
- 標準有理式(CRE)形
普通に入力している多項式は一般形になるようです。CRE形は「多項式をリストによって再帰的に表現する形式」みたいです。要は「無限にいたる」表現ができそうなもの。それを示すシンボルに2種あり。
-
- /R/ 標準有理式(CRE)形を示すシンボル
- /T/ テイラー級数の表現に使われる拡張CRE形を示すシンボル
だそうです。分かったような分からぬような。。。ともあれ/T/がついているときは無限に至るルートを残しつつ、先っぽだけ表示したもん、じゃないかと。実際、先ほどの/T/シンボル付きの表現を以下の関数に引き渡すと指定された項からあとはバッサリと切られてフツーの多項式となります。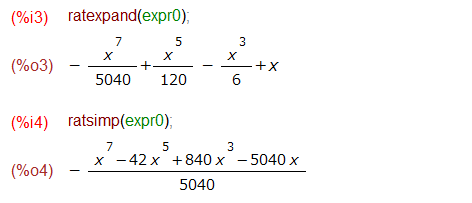
素直に多項式にするratexpand()と、通分しちゃうratsimp()。ホントか?
さて、マクローリン展開できるならば、近似値を求めることもできる筈、ということで求めてみました。こんな感じ。
π/2 = 90°は、マクローリン展開しているポイントの0からは結構離れてはいるような気がするものの、sin(90°)は1なので、結構いい線の近似値が計算できている気もします。なお、マクローリン展開した結果を関数として定義するのに define 使いました。:= で関数定義しようとしても上手く行かなかったです。なんでだろ~。
マクローリン展開を応用して極限を求める
さて、Maxima様の上でマクローリン展開できる気がしてきたので、マクローリン展開つかって極限(limit)を求めてみることにいたしました。テキトーな例題ないかな~と探していて見つけたのが以下です。
弱点克服 大学生の微積分 江川著 東京図書 P.50
上記ページから見つけた極限の例題が以下の(%o11)です。なお、Maxima様に式を書いてもらうと { } が無くていささかみずらかったので、後から手で{ } を書き加えてます。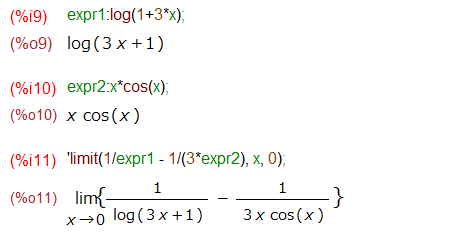
また、後の計算で参照しやすいようにexpr1、expr2などというものを定義してそれで記述してます。
さっそく、expr1、expr2をマクローリン展開してみます。こんな感じ。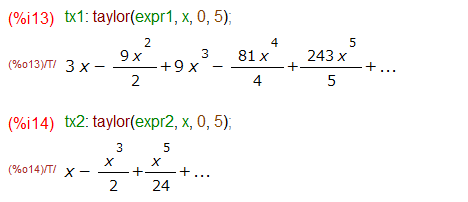
例によって /T/ シンボルがついた無限級数をxの5乗の項で打ち切った表現です。マクローリン展開した結果で例題のlimitの{}の中の関数を置き換え、ついでにratsimpまでかけて通分して整理してみます。そして極限を求めてみる、と。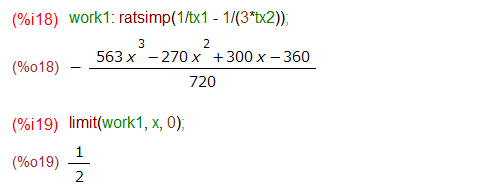
お答え「2分の1」でました。あっているみたいです。
なお、上記のようにわざわざ自力でマクローリン展開して途中経過を刻まなくても、以下のように元の表現のままでMaxima様に極限求めて、とお願いしても一撃でお答えが返ってきます。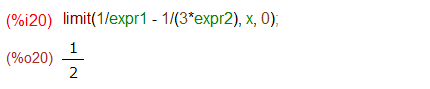
なんだかな~