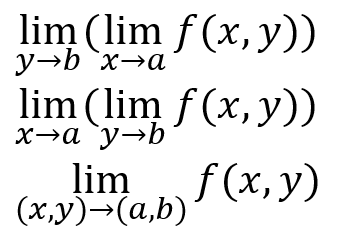今回より、多変数関数に突入、ようやくです。偏微分したり重積分したりと前途洋々(多難?)であります。まずは極限から。Maxima様には極限を求めるlimit関数ありますが、調べたところでは多変数対応ということはないみたい。でもま、定石どおりに処理すれば(するのはMaxima様ですが)できないことはないっと。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
いつもお世話になっております、Maximaの日本語マニュアルページは以下です。
2変数関数の極限
1変数のときの極限も上(plus)から近づくとか下(minus)から近づくとかありました。しかし2変数関数の極限はメンドクセー奴です。上下に加えて各変数を個別にlimitとる順番でも極限値が違うことがあるとか、順番に適用でなくて2変数を同時に近づけたらどうよとか、いろいろありーのです。
例題その1
まずは素性の良いお題から。極限とるターゲットは以下のようです。
最初は、xとyバラバラに、順番つけて極限とってみます。Maxima様がしつこく極限とらない側の変数がpositiveなの、negativeなのとお聞きになられます。イチイチ指定(両方とも)していたらケースが膨れあがりました。ケースは分かれてもお答えは皆0です。一致してよかった。
さて、個別に x,y 毎適用するのではなく、どんな方向からでも近づけるにはどうしたらよいか?そこは教科書に記載の定石?でx、y座標を極座標表示に変換してやって 動径 r を0にもっていくと1変数対応のlimit()関数でも計算できるようになりました。極座標に変換するの、も少しカッコよくできないのか?とりあえず、こんな感じ。
この方法でもlimitは0。ということは極限値0で良いのね。知らんけど。
例題その2
当然素性が良いものばかりでは片手落ちということで、次は素性の良くないケースです。見た目はその1より簡単そうに見えますが。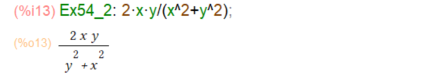
x, yの順でも、y, xの順でも同じお答えと期待を持たせておいて、やはり極座標表示で一気にやってみると。
limitとったあとの三角関数の式、どうしようかと一瞬青ざめましたが、trigrat()一発で整理ができたのでハッピー。まあ高校で習った公式をちゃんと暗記している人には何でもない整理だけれども。
しかし sin(2Θ)ってことは0じゃないじゃん。たまたまΘ=0の方角からかΘ=πの方角からか近づいたらば0だけれどもそうでなければ角度によって違う値をもつみたいっす。ということは極限値は存在しない(収束しない)ってこと?