別件で正規分布「ではないやつ」のリサンプリングが分からんとブーたれていたらバチがあたりました。今回の積分の課題は正規分布に至る道筋デス。前回は特異点をすり抜けて?積分。今回は-∞から∞までの広義積分であります。「ありがち」か?教科書はテクを駆使して解いてますが、Maxima様にお願いすれば一撃。あっけない?
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
今回の例題
今回の例題は以下です。このところ二重積分だの、三重積分だのを練習してきたのに積分記号が1個しかありません。ものたらない?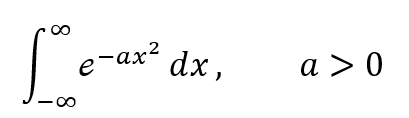
いえいえ、教科書では二重積分にした上で極座標変換を駆使して上下から「はさみうちの原理」で計算してます。これまた自分じゃゼッテー解けない奴だな。
まずはグラフを描いてみる
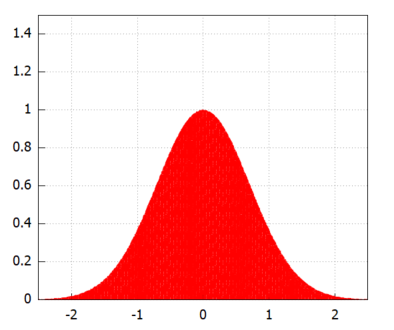
とりあえず上の定積分の「雰囲気」をグラフにしてみます。定数 a ではグラフにできないので a=1 とテキトーに値を入れた上で、xは、-∞から∞を -2.5から2.5とバッサリなグラフです。描くのは以下で。
draw2d(x_voxel=100, y_voxel=100, grid=true, region(y<=%e^(-x^2), x, -2.5, 2.5, y, 0, 1.5))
この形、どっかで見たことないか。そうです正規分布の確率密度関数のグラフとよく似てますな。ただしピークが1になっているので、正規分布をY方向上に引き伸ばしたような形みたいっす。
そういうことで(どういうことだ?)、母平均μと母分散σ2の正規分布の確率密度関数の式を以下に掲げます。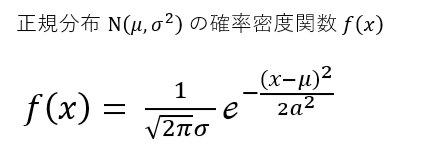
数学素人の年寄があれこれ言うのも何なので、正規分布を忘れていたよゐこのためにURLを貼り付けておきます。産総研様のありがたいページです。
さて上記のf(x)は「確率密度関数」なので、計算しなくても(本当はできなくても)以下が成り立つことは明らか。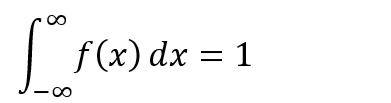
例題の前にそう言っておいてくれよ。
Maxima様にお願いすれば一撃
さてどう見ても例題の積分は「有名すぎる」関数なのでMaxima様が積分できないなどとは考えられませぬ。教科書ではテクを駆使してますが、素のままお願いしても解けるじゃろうて。こんな感じ(例によって積分直前でスンドメして積分記号を味わうスタイル。)
事前のassume忘れたので、途中で聞かれてしまいましたが、答えは出たと。
同様に正規分布の確率密度関数を-∞から∞まで積分してみるとこんな感じ。
結果は1。目出度い。