頭の固い年寄デス。面積求めるのに二重積分を持ち出すこともあるまい、と思っていました。しかし、今回は二重積分でも面積求まるのだぞ、それもカッコよくという回なんであります。言われてみれば当たり前なんだが。それに変数変換にヤコビアンさんにと数学センスの無いこの年寄は取り残されてる感じ。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書（参考書、問題集？）の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
二重積分で面積が求まるとはこれ如何に
領域Dを二重積分したら求まるのは体積だろ～と思っていたら、目から鱗。積分関数が「１」であれば、厚さ「１」底面積Dの体積だから、それは面積Sと等しいのよ、と。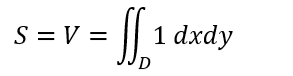
当たり前っちゃ、当たり前だけれど、頭の固い年寄には思いつきもせず。
今回の例題
さて、そういうことでの今回の例題は以下です。以下の４曲線で「囲まれている」部分の面積を求めよと。何やらメンドクセー。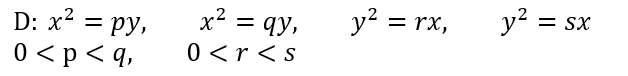
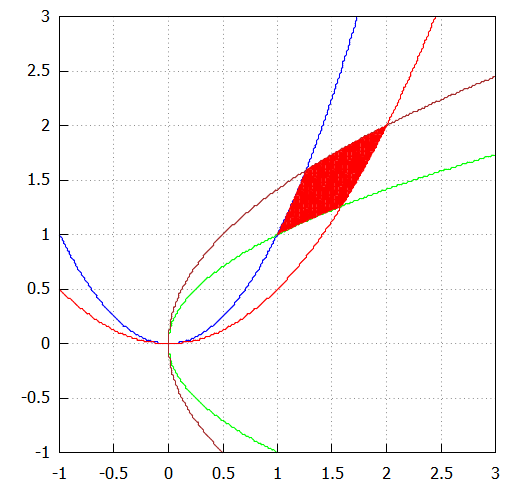
まずは「囲まれている」のがどの辺なのよ、ということを年寄の身に染みるように、グラフを描いて考えます。描いてくれるのはMaxima様だけれど。例によってp, qなどの定数には具体的な数値をあてはめないと描けないので、適当に、１，２，１，２などと割り当ててます。こんな感じ。
L1: x^2=p*y; L2: x^2=q*y; L3: y^2=r*x; L4: y^2=s*x; p: 1; q: 2; r: 1; s: 2; draw2d( color=blue,implicit(L1, x, -1, 3, y, -1, 3), color=red,implicit(L2, x, -1, 3, y, -1, 3), color=green,implicit(L3, x, -1, 3, y, -1, 3), color=brown,implicit(L4, x, -1, 3, y, -1, 3) )
さて、とりあえず「曲線の」グラフはこんな感じ。
「囲まれている」面積を塗りつぶすのは、こんな感じ。ようやっと region()慣れてきたわいなあ。
draw2d(x_voxel=100, y_voxel=100, grid=true, proportional_axes = xy, color=blue,implicit(L1, x, -1, 3, y, -1, 3), color=red,implicit(L2, x, -1, 3, y, -1, 3), color=green,implicit(L3, x, -1, 3, y, -1, 3), color=brown,implicit(L4, x, -1, 3, y, -1, 3), region(x^2-p*y > 0 and x^2-q*y < 0 and y^2-r*x > 0 and y^2-s*x < 0, x, -1, 3, y, -1, 3) )
塗りつぶした様子が以下に。
これをチマチマと場合分けなどしていけば、二重積分などせずとも面積は求まる筈（中学生、いや高校生の問題？）
変数変換
しかし、教科書の解法はスマート。以下のように変数変換するのです。まあ、この形は元の積分範囲の定義の式みたら出てくるのだろうけど、頭の固い年寄には思いつきもいたしやせん。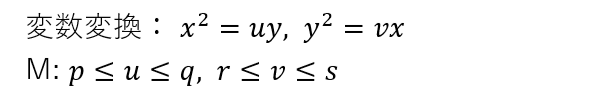
そして、驚くことに変数変換後の積分範囲M、単なる「四角形」になっているじゃございませんか。魔法のような。
変数変換したので、例によってヤコビアンさんを求めてやれば積分は出来たも同線。しかし、変換後の変数 u, v でx, yを記述するのはメンドイです。そうしたらば再び目から鱗。変数x, yでu, vは既に書けているので、逆転の発想、ひっくり返したヤコビアンさんを求めた後で逆数とれば良いのでないかい、と。これはまた。こんな感じ。
あれよあれよという間もなくヤコビアンさんが求まりましたです。これまた魔法のような。
面積を求める
さて面積を求めるための「二重積分」してみます。あんまり簡単な積分になりすぎていつもの「スンドメ」スタイルで積分記号を一端味わうところでは止まらなかったです。お答えが以下に。
あれよあれよ。