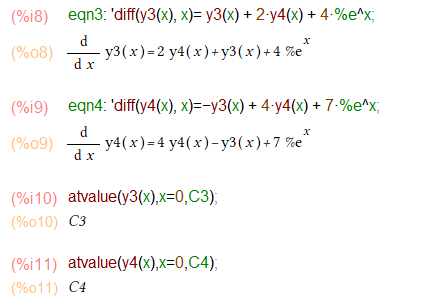今回から1階連立微分方程式の練習に入ります。教科書では2階の微分方程式を2個未知関数の1階連立微分方程式に変換したり、逆に一階の連立微分方程式から2階の微分方程式に変換できることが示されとります。なんだかな~。察するに伝家の宝刀 ode2は使えない雰囲気がありあり。desolve関数に御出馬願うしかない?
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書の例題をMaximaの練習に使わせていただいております。ただし御本家『培風館』様のホームページで検索してみるも掲載されていないようです。絶版? そのため以下のリンクは『Amazon』の通販ページであります。ご注意を。
※MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
n次正方行列とn次ベクトル関数による問題の表記
太線文字で書けばベクトルね。それも列ベクトル。数学らしいっす。f(x)がノンゼロならば非同次、0ならば同次と呼ぶと。美しいですが、解ける気がしないです。
でもね、Scilab/Xcosのような数値シミュレーションで微分方程式を解くときに、単なる積分ブロック一種類で複雑なシステムに立ち向かえるのは、元が2階だろうと3階だろうと結局1階の連立に帰着できる、というありがたい性質のお陰でないかと。閑話休題。
最初の例題
最初の例題は以下です。eqn1とeqn2の連立微分方程式です。desolve関数には微分方程式を束(リスト)にして食わせることができるので、2本だろうが、3本だろうが、束にして渡すことが可能です。ただし、以前にも書きましたが、ode2関数とは異なり、未知関数がどの独立変数の関数なのかをアカラサマに書かないと解いていただけませぬ。ode2では、y一文字で済んだところを y(x)のように明示することが必要です。また、ode2では一般解を求めるのにテキトーに任意定数を生成してくれたのですが、desolveの場合はy(0)とかイチイチメンドイ記法で定数をハメコンできます。1個くらいならy(0)もいいですが、方程式が増えると何やら複雑となります。せめて文字定数で書いて、ということでatvalue関数で事前に定数を文字で定義してます。
解くこと自体は簡単、desolve関数にリストに入れて束ねた方程式と、求めるべき関数名のリストを与えるだけです。こんな感じ。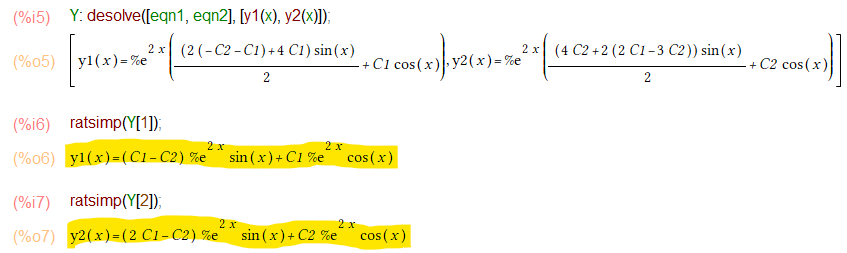
desolveは、リストに入れた形でお答えを返してくれる上に、結果の見栄えをよくするような整理までしてくれないみたいです。そこで結果の各関数を個別に取り出して ratsimpにかけて整形してます。
2番目の例題で不思議な質問?
しかし、問題は desolveに上記を渡したときに身に覚えのない g668などという変数が、正なの負なのゼロなどと聞かれました(黄色のマーカ。)これは何? 試みに、p、n、zみな入力してみましたが、得られるお答えは同じものみたいでした。何なんだろ~。
結果そのものは有っているみたいなので、上記同様、1関数ずつとりだしておきました(緑のマーカ。)
なお、お答えをみるとC3、C4で書かれた定数を別な定数にまとめたいです。こんな感じかな。
-
- y3(x)=Ae3x – 2Be2x + ex
- y4(x)=Ae3x – Be2x -2ex
こういうところは 「ode2方式」の方がありがたいが。。。