今回は１階連立微分方程式の初期値問題です。前回から何度目か再登板のdesolve関数。もともとが初期値、境界値問題を解きやすく？できているように思います。一般解を求める時のように解いた後で整理するようなメンドイことは不要。ほとんど何もせずとも初期値問題の解答が得られるっと。ハマリどころってやつ？
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書の例題をMaximaの練習に使わせていただいております。ただし御本家『培風館』様のホームページで検索してみるも掲載されていないようです。絶版？ そのため以下のリンクは『Amazon』の通販ページであります。ご注意を。
※MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
最初の例題
最初の例題を解くための手順をテキストで書いておきます。
-
- 最初に連立方程式の一つ目を eqn1というお名前で定義、２つ目を eqn2というお名前で定義します（お名前は何でも良いです。）
- 定義の際、忘れずに微分のdiffの先頭に ‘ をつけてその場で評価されないようにしておきます。
- 独立変数が何なのかハッキリするように y1(x) みたいな形で求めるべき関数どもを記述します。xに対する関数y1てことだね。
- そして atvalue関数で、x=0のときの関数初期値を与えます。
- 後は desolveに提出するのみ。
eqn1: 'diff(y1(x), x)=3*y1(x) + 2*y2(x); eqn2: 'diff(y2(x), x)=3*y1(x) - 2*y2(x); atvalue(y1(x),x=0,3); atvalue(y2(x),x=0,-2); Y: desolve([eqn1, eqn2], [y1(x), y2(x)]);
結果が以下に。黄色のマーカ部分が初期値問題の解です。
２番目の例題
２番目は１番目よりちょっと複雑になってますが手順は同じ。問題の入力部分が以下に。ここまでの部分は最初の問題と同じ手順ね。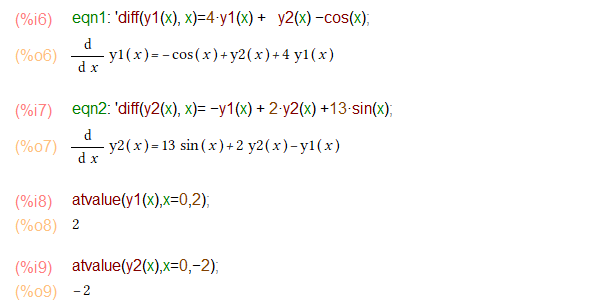
desolveに解答いただいた結果が以下に。
desolveの結果が若干「整理されていない形」であったので、上記では関数を一つづつ取り出して ratsimpにかけて整理してます。これで「教科書が期待している形」のお答えになりましたです。
実際には、ratsimp()にリストを渡してもよきに処理してくれるので、
ratsimp(Y)
で、リストの形のまま解を得ることもできます。どっちも変わらんけど。