前回は、複素インピーダンスをベクトル表示ということで、複素平面上に「矢印」でベクトル表示をしてみました。いい感じ?でもベクトルとして実体を見せるためには特定の周波数を指定する必要があります。どっちかっていうと「周波数応答」が知りたいのだな~ということで、周波数応答プロット用の関数を追加。
※「やっつけな日常」投稿順 Index はこちら
※動作確認は、パソコン上の wxMaxima 22.04.0 および Androidスマホ上の Maxima on Android 3.2.1 で行っています。
またもや前回のチョイ直し
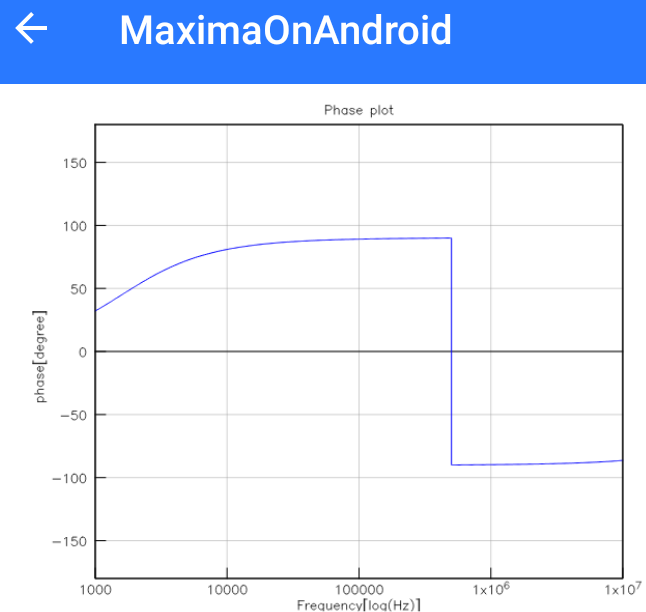
またもや前回のチョイ直しです。これによって以下のmagnitude(複素インピーダンスに適用すれば絶対値)とphaseのグラフが描けるようになりました。以下はパソコン上ではちゃんとΩが表示されていたのですが、MoAに持っていく過程で文字コードがなんやら化けていて、Ωが四角になってしまってます。抜けてるな~、要修正。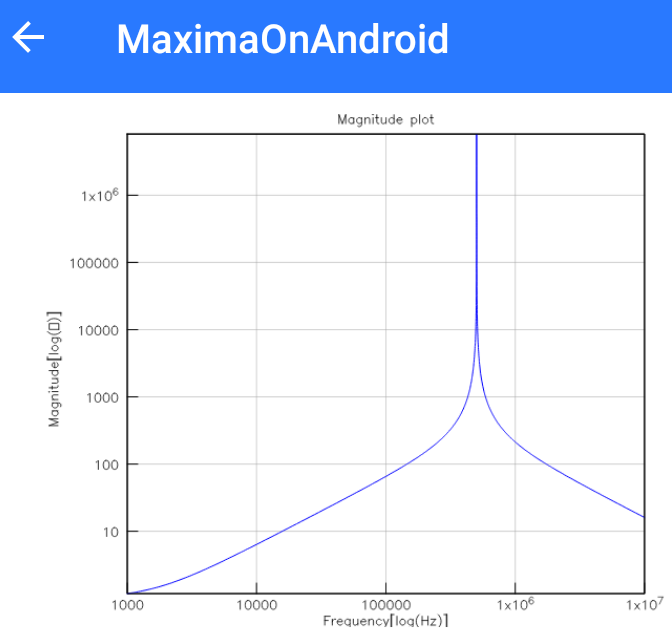
先に生成したグラフを出しておいて、後から目標グラフです。以下はLTspiceでシミュレーションしたもの。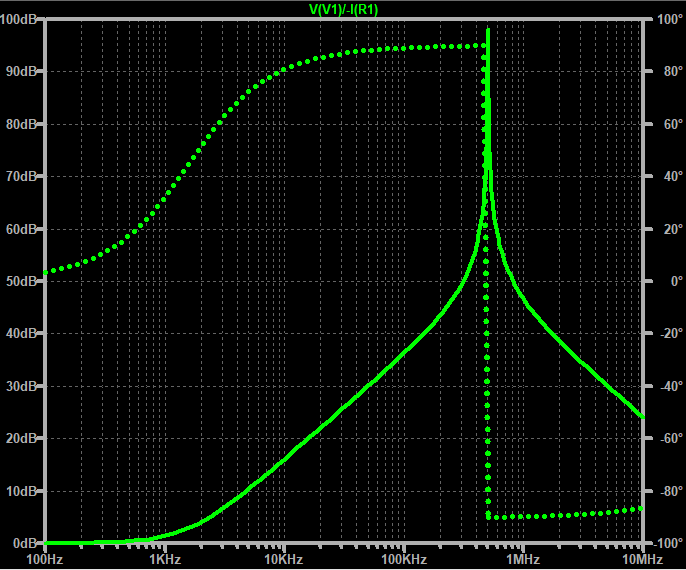
形はだいたいOK。ただピークはMaxima側では鋭く高いです。SPICEは描画範囲をただだか100点くらいの計算点で描いているので、点と点のスキマのところはナシってことみたいです。
前回関数、今回新設関数の使い方
前回はインピーダンスを定義するための ser(直列接続)、par(並列接続)、ci(キャパシタンス)、ii(インダクタンス)の関数を使ってインピーダンスZを文字で定義。そのあと、at関数で文字に具体的な値を当てはめて浮動小数としてZfを求めました。その結果を plotImpedance関数に渡せばベクトル表示ができると。
Z: ser(par(ci(C1), ii(L1)), R1); Zf: float(at(Z, [C1=1e-9, L1=100e-6, R1=1, f=1000])); plotImpedance(Zf);
今回はZfを求めるところでC、L、Rには具体的な数値を与えてますが、周波数fは文字のまま残しておきます。こういうことが出来るのが数式処理ソフトウエアの強みだなあ。
そして周波数fを変数として含んだままのZfを plotMag関数に渡せば周波数応答プロットを求めてくれます。なお2番目の引数に渡すリストはプロットする周波数の[下限, 上限]です。
Zf : float(at(Z, [C1=1e-9, L1=100e-6, R1=1])); plotMag(Zf, [1e3, 10e6]);
なお、plotPhase関数に同じ引数を渡せば位相の周波数応答が描かれます。
複素インピーダンス表示のソースコード(チョイ直し)
パソコン上のMaximaでも、スマホ上のMaximaでも同じソースで動作します。
/* Maxima BATCH FILE 2024/05/21 J.Halfmoon */
/* Display impedance */
algebraic:true$
/*- Utilities -----------------------------------*/
log10(x) := log(x)/log(10)$
roundF(x, p) := float(round(x*10^p)/10^p)$
dB(Vout, Vin) := float(20*log10(Vout/Vin))$
phase(z) := 180*carg(z)/%pi$
vec2(x, y) := matrix([x],[y])$
mat22(a11, a12, a21, a22) := matrix([a11, a12],[a21, a22])$
vecP(v2) := vector([0, 0], [v2[1, 1], v2[2, 1]])$
vecLis(lis) := if listp(lis) then map(vecP, lis) else [vecP(lis)] $
vi: vec2(1, 0);
vj: vec2(0, 1);
I: mat22(1, 0, 0, 1);
/*- impedance calculation -----------------------*/
define(ser ([Lis]), '(apply ("+", Lis)))$
define(par ([Lis]), '(1 / (apply ("+", 1/Lis))))$
ci(C):= 1/(%i*2*%pi*f*C)$
ii(L):= %i*2*%pi*f*L$
/*- plot impedance vector ------------------------*/
plotImp(vP1, vP2, xR, yR) := draw2d(
xrange=xR, yrange=yR, proportional_axes=xy,
xaxis=true, yaxis=true, grid=true,
title = "Impedance Z",
xlabel = "Real", ylabel = "Imag",
color = blue, head_length = 0.2, head_angle = 20,
color = blue,
vecLis(vP1),
color = red,
vecLis(vP2)
)$
prSub(z) := ceiling(max(realpart(z), imagpart(z)) * 1.2)$
plotImpedance(z) := block([tmp],
tmp: prSub(z),
XR: [-0.1, tmp],
YR: [-tmp, tmp],
vZ: [vec2(realpart(z), 0), vec2(0, imagpart(z))],
vY: vec2(realpart(z), imagpart(z)),
plotImp(vZ, vY, XR, YR)
)$
/*- magnitude plot -----------------------------------*/
plotMag(zf, fR) := draw2d(
xrange=fR,
xaxis=true, yaxis=true, grid=true, logx=true, logy=true,
title = "Magnitude plot",
xlabel = "Frequency[log(Hz)]", ylabel = "Magnitude[log(立)]",
explicit(abs(ev(zf, f=x)), x, fR[1], fR[2])
)$
/*- phase plot -----------------------------------*/
plotPhase(zf, fR) := draw2d(
xrange=fR, yrange=[-180, 180],
xaxis=true, yaxis=true, grid=true, logx=true, logy=false,
title = "Phase plot",
xlabel = "Frequency[log(Hz)]", ylabel = "phase[degree]",
explicit(phase(ev(zf, f=x)), x, fR[1], fR[2])
)$
/*- Example -------------------------------------*/
Z: ser(par(ci(C1), ii(L1)), R1);
/* Zf: float(at(Z, [C1=1e-9, L1=100e-6, R1=1, f=1000])); */
/* plotImpedance(Zf); */
Zf : float(at(Z, [C1=1e-9, L1=100e-6, R1=1]));
plotMag(Zf, [1e3, 10e6]);
/* plotPhase(Zf, [1e3, 10e6]); */