前回はもったいなくもMaxima様にチンケなベクトルを３次元表示していただきました。３次元のベクトルが表示できるのだから、外積など計算してこれまたベクトル表示できるよね。ついては元のベクトル２つも描く「ついでに」２つで定義される平行四辺形を描き、外積ベクトルがそれに直交している雰囲気だしたいです。欲張りだな。
※「やっつけな日常」投稿順 Index はこちら
※動作確認は、パソコン上の wxMaxima 22.04.0 および Androidスマホ上の Maxima on Android 3.2.1 で行っています。
外積ベクトルの表示
ベクトルの内積はスカラーですが、外積はベクトルです。そして外積する２つの入力ベクトルと直交している方向となるので３次元でないと描けませぬ。数学素人のお惚け老人が何をか言わんや。Windows11機上のMaxima（実際にはGnuplot）で描いた図が以下です。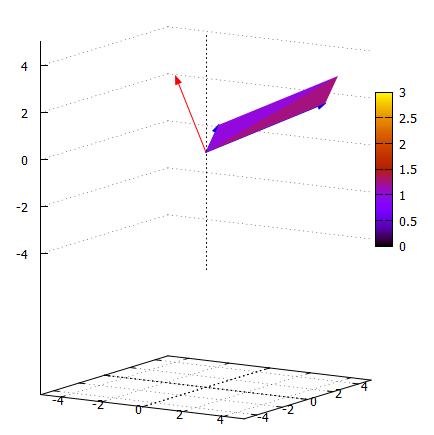
例によってWindows上でならば、視点を変えることも簡単。こんな感じっす。
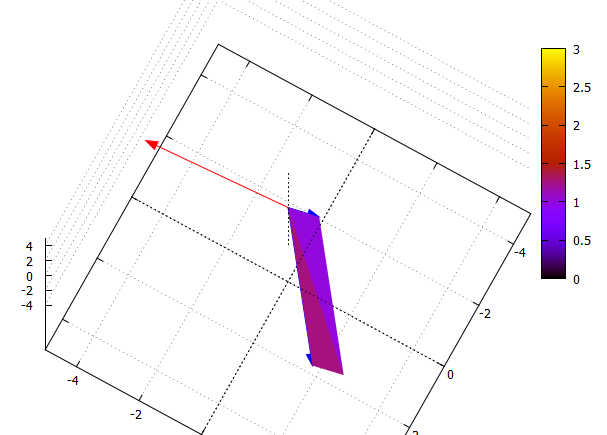まあ、今回のミソは、２つの入力ベクトルが生成するひし形をどう３次元空間でdraw3dするか、というところでした。ちょっと手間取ったです。
今回使用のMaximaソース
前回の素の３次元ベクトル表示用のソースに外積を計算する関数（どうも自分で作れ、ということみたいっす）とそれを使ってプロットする関数を加えたものが以下に。なお、中途半端な長さで揃えたコメント行がところどころに入ってますが、手元のスマホのエディタで、フォントをMonospaceの11ポイントにするとだいたい画面いっぱいになる感じにしてあります。パソコン上で編集するときの目印的な感じ。
/* Maxima BATCH FILE 2024/05/23 J.Halfmoon */
/* Display 3D vectors */
/* Update: 2024/05/24 outerProduct */
algebraic:true$
/*- Utilities -----------------------------------*/
log10(x) := log(x)/log(10)$
roundF(x, p) := float(round(x*10^p)/10^p)$
dB(Vout, Vin) := float(20*log10(Vout/Vin))$
vec3(x, y, z) := matrix([x],[y],[z])$
mat33(a11, a12, a13, a21, a22, a23, a31, a32, a33)
:= matrix([a11, a12, a13],[a21, a22, a23],[a31, a32, a33])$
vecP3(v3) := vector([0, 0, 0], [v3[1, 1], v3[2, 1], v3[3,1]])$
vecLis3(lis) := if listp(lis) then map(vecP3, lis) else [vecP3(lis)] $
/*- plotvec ------------------------------------*/
plotVec3(vP, xR, yR, zR) := draw3d(
xrange=xR, yrange=yR, zrange=zR,
proportional_axes=xyz,
xaxis=true, yaxis=true, zaxis=true,
color = blue, head_length = 0.2, head_angle = 20,
vecLis3([vec3(1, 0, 0), vec3(0, 1, 0), vec3(0, 0, 1)]),
color = red,
vecLis3(vP)
)$
plotVec32(vP, vQ, xR, yR, zR) := draw3d(
xrange=xR, yrange=yR, zrange=zR,
proportional_axes=xyz,
grid=true,
xaxis=true, yaxis=true, zaxis=true,
color = blue, head_length = 0.2, head_angle = 20,
vecLis3([vec3(1, 0, 0), vec3(0, 1, 0), vec3(0, 0, 1)]),
color = green,
vecLis3(vP),
color = red,
vecLis3(vQ)
)$
/*- outer product ------------------------------*/
outerProd(v1, v2) := vec3(
v1[2,1]*v2[3,1] - v1[3, 1] * v2[2, 1],
v1[3,1]*v2[1,1] - v1[1, 1] * v2[3, 1],
v1[1,1]*v2[2,1] - v1[2, 1] * v2[1, 1]
)$
plotOuterProd(v1, v2, xR, yR, zR) := block( [t1, t2],
t1: v1 + v2,
t2: outerProd(v1, v2),
draw3d(
xrange=xR, yrange=yR, zrange=zR,
proportional_axes=xyz,
grid=true,
xaxis=true, yaxis=true, zaxis=true,
enhanced3d = true,
triangle([0,0,0],[v1[1,1],v1[2,1],v1[3,1]],[t1[1,1],t1[2,1],t1[3,1]]),
triangle([0,0,0],[v2[1,1],v2[2,1],v2[3,1]],[t1[1,1],t1[2,1],t1[3,1]]),
color = blue, head_length = 0.2, head_angle = 20,
vecLis3([v1, v2]),
color = red,
vecLis3(t2)),
t2
)$
/*- Example ------------------------------------*/
XR: [-5, 5]$
YR: [-5, 5]$
ZR: [-5, 5]$
vi: vec3(1, 0, 0);
vj: vec3(0, 1, 0);
vk: vec3(0, 0, 1);
v0: vec3(4, 3, 2);
v1: vec3(0, 1, 1);
I: mat33(1, 0, 0, 0, 1, 0, 0, 0, 1);
Rx: mat33(1, 0, 0, 0, 0, -1, 0, 1, 0);
vN: Rx . v0;
/* plotVec32(v0, vN, XR, YR, ZR); */
plotOuterProd(v0, v1, XR, YR, ZR);
MoA(Maxima on Android)上での実行
例によってMoAで実行しても基本的にはWidows版と同じ「図」が得られます。ただし、拡大縮小はできますが、視点変更はスクリプトを直さないとダメみたいっす。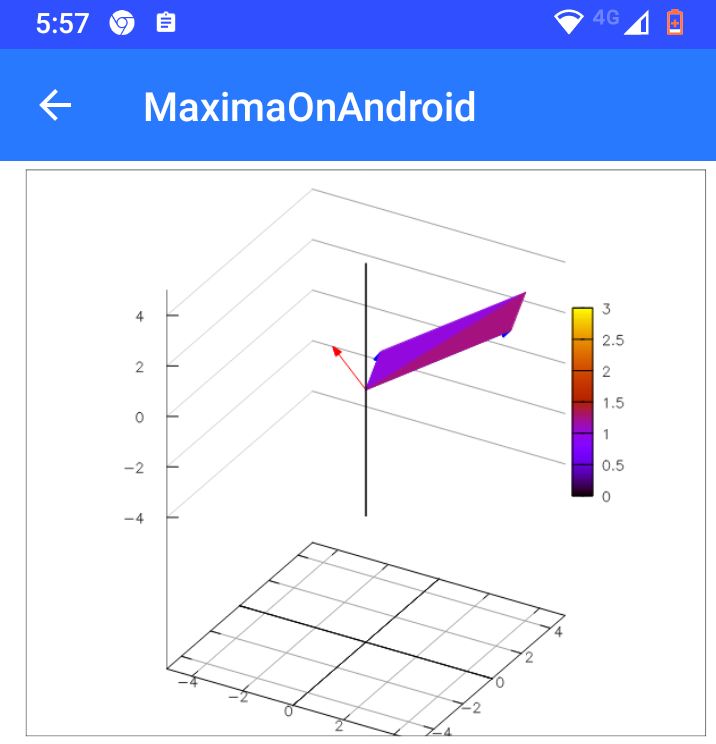
なお、plotOuterProd関数はプロットの裏側で計算した外積ベクトルを返してきます。こんな感じね。
ついでなのでスマホ上で上記のスクリプトを編集（大したことはしないデス。数字を書き変えるくらい）している様子が以下に。
このひし形な感じをプロットしたかったのよ。。。