
今回は、教科書的には「行列の対角化」を利用して一階の連立微分方程式を「簡単」にして解いちまおう、の件です。しかし、Maxima様にお願する場合にはdesolve一発、何の工夫もなし。ただ、desolveは境界値問題には良いですが、一般解を求める場合、教科書的なお答えにするのに一手間いることがあるっと。そんだけ。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書の例題をMaximaの練習に使わせていただいております。ただし御本家『培風館』様のホームページで検索してみるも掲載されていないようです。絶版? そのため以下のリンクは『Amazon』の通販ページであります。ご注意を。
※MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
行列を使った定数係数1階連立線形微分方程式の表現
そこで登場する行列Aであります。その行列Aが「実対角化可能な場合」、つまりは「例のPPAPじゃなかったP-1APで」対角行列Bが求まるならば、
解を求めることができる、らしいです。
でもま、desolveにお願いするので、そういった「頭を使う必要」はぜんぜんありません。馬鹿になるばかりだな。。。
最初の例題
最初の例題は境界値問題です。教科書的には行列Aの固有値を求めて、Pを決めてという塩梅で話が進むのですが、何もなし。
desolve的にはツボにハマりどころなので、一撃です。上記の黄のマーカ部が解ね。
第2の例題
次は一般解を求める問題です。「とりあえず」atvalue関数で境界条件にテキトーな定数 K1、K2など突っ込んでます。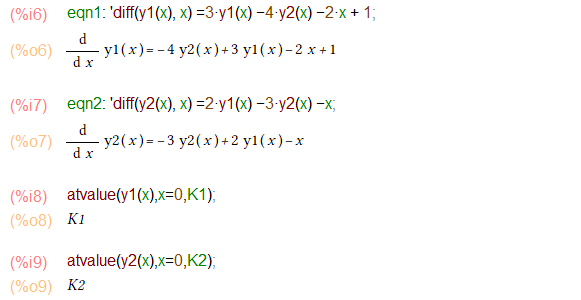
すると当然ながら desolveした結果にあらわれてくる「定数部分」はケッコー複雑です。教科書的なスッキリした定数にまとまってません。そこで以下のように後付けの substにてスッキリ化?してます。こんな感じ。
黄色のマーカ部が教科書的にOKな感じの解です。表面的にはまったく固有値も対角行列も出てこないけど解けるっと。desolveのお陰です。

