前回、空気抵抗の無い時の自由落下をplotdfしてみました。今回は空気抵抗のある場合です。しかし、気づいてしまいました。高校の時に教わった「空気抵抗が速度に比例する」というドグマ？が成立するのは極めて狭い範囲だということを。「フツー」の時は速度の二乗に比例するじゃん。レイノルズ数登場。流体の沼にハマってしまうのか？
※「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwx Maximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
空気抵抗
忘却力の年寄は、最近のことは直ぐに忘れてしまいますが、昔覚えたことは忘れないのです。遥かな古代、高校の物理でならった「空気抵抗は速度に比例する（もちろん速度と反対の方向ね）」という金科玉条に縛られてました。まあね、流体の中の運動なので一筋縄ではいかず、
-
- 空気抵抗が速度に比例するケース（粘性抵抗）
- 物体の速さが遅い
- 物体の大きさが小さい
- 空気抵抗が速度の二乗に比例するケース（慣性抵抗）
- 物体の速さが早い
- 物体の大きさが大きい
- 空気抵抗が速度に比例するケース（粘性抵抗）
の両方があることは朧気に認識してはおりました。でもま、高校でならったし、フツーにボールを落とすような範囲では速度に比例するとして計算して当たらずとも遠からず、などと思い込んでおったのでございます。
しかし、それに一石を投じて下すったのが以下の御研究でございます。『奈良教育大学学術リポジトリ』様、
上記の御研究は、勿論微分方程式を使って論じられている部分があるのですが、わざわざ？風洞実験までやっておられます。これなら物理で微分方程式を使ってはいけないらしい？高校生も出来る？（風洞使える方が珍しいか。）
上記をよんで目から鱗であります。そしてレイノルズ数の御登場です。上記の論文から引き写させていただいた、ボール（玉）のレイノルズ数の式が以下に。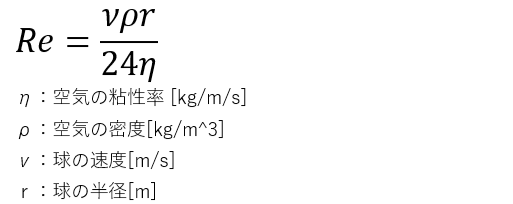
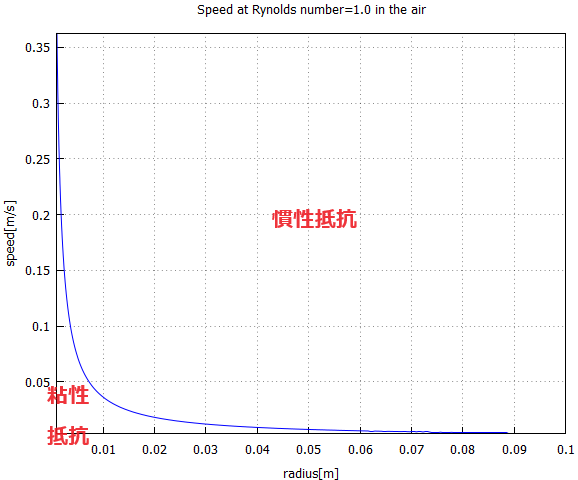
レイノルズ数が小さい（＜１）なら粘性抵抗が主、レイノルズ数が大きい（＞１）なら慣性抵抗が主であります。
ηとρは定数とみなしてしまい、Re＝１とおけば、粘性と慣性が拮抗する（Re＝１）のグラフを引けるハズ。計算してみたのが以下に。
上記でdraw2dしてみたグラフが以下です。
横軸は球の半径、縦軸は落下速度であります。なんだ、半径１ｃｍのボールが毎秒５ｃｍで落ちたら、粘性抵抗で計算できる範囲を超えているじゃん。「空気抵抗は速度に比例」とおもって計算できる部分って人間的な尺度からすると限りなく「薄い」エリアだな。
今回は１０００ｍの上空から空気抵抗のある落下をplotdfしようとしているので、使う式は「速度の二乗に比例」だな。まあ、計算簡単なので「速度に比例」のグラフも描いてみますか。
plotdf
さて、plotdfで使った「空気抵抗のある落下」の設定が以下です。
まずは速度の二乗に比例する本命版
plotdf([-g+c2*v^2, v],
[v, h],
[parameters,"g=9.8,c2=0"],
[nsteps, 1000],
[sliders,"c2=0:0.1"],
[trajectory_at,0,1000],
[v, -200, 0],[h, 0, 1000])$
なお、簡単のため、係数 c2 は本来 k / m のように表される数です。kは[kg / m]で表されるような空気抵抗係数、mは質量[kg]ね。
つづいて速度に比例する「対抗」版
plotdf([-g-c1*v, v],
[v, h],
[parameters,"g=9.8,c1=0"],
[nsteps, 1000],
[sliders,"c1=0:0.25"],
[trajectory_at,0,1000],
[v, -200, 0],[h, 0, 1000])$
まずは、両方の版でc1=0, c2=0、つまり空気抵抗なしの単純自由落下のときのplotdfグラフが以下に。縦軸が落下高さh [m]、横軸が落下速度v[m/s]です。前回同様、上向きが＋ね。左が（ここでは空気抵抗０だけれども）空気抵抗が速度比例の設定の方、右が速度の二乗に比例の設定の方デス。同じ結果だよ。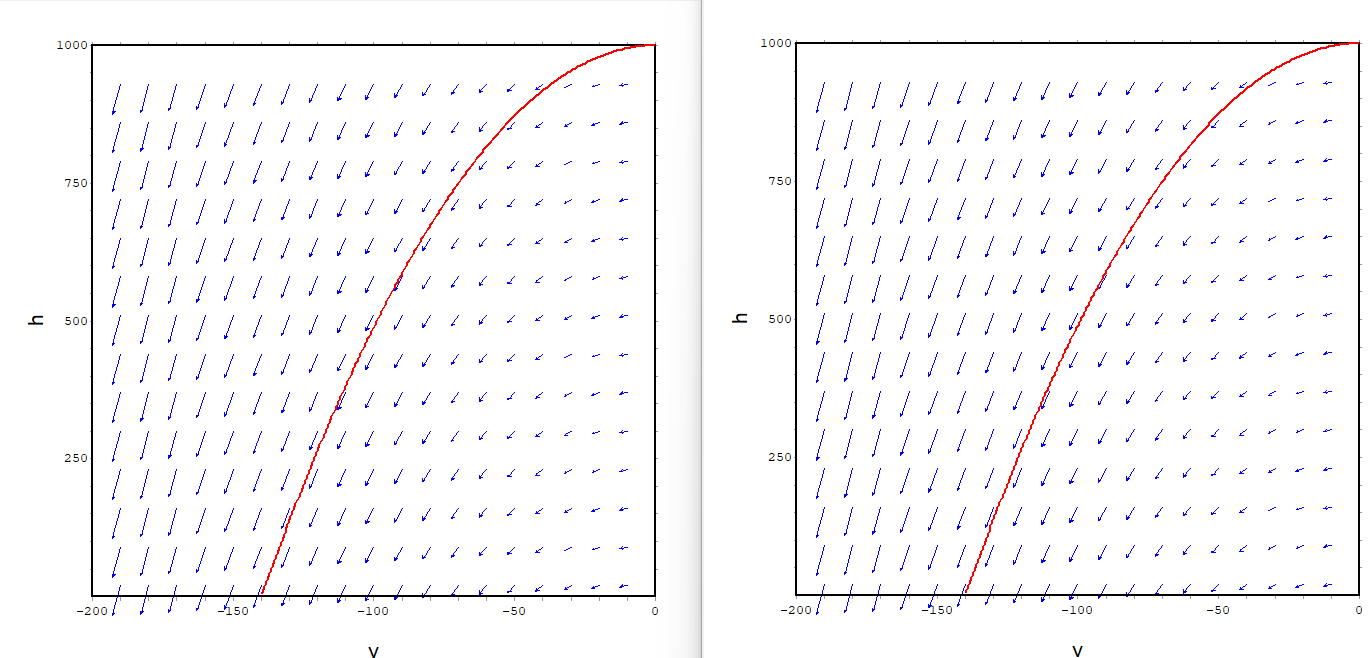
さて、c1=0.01、c2=0.01としてみました。するとグラフはこんな感じ。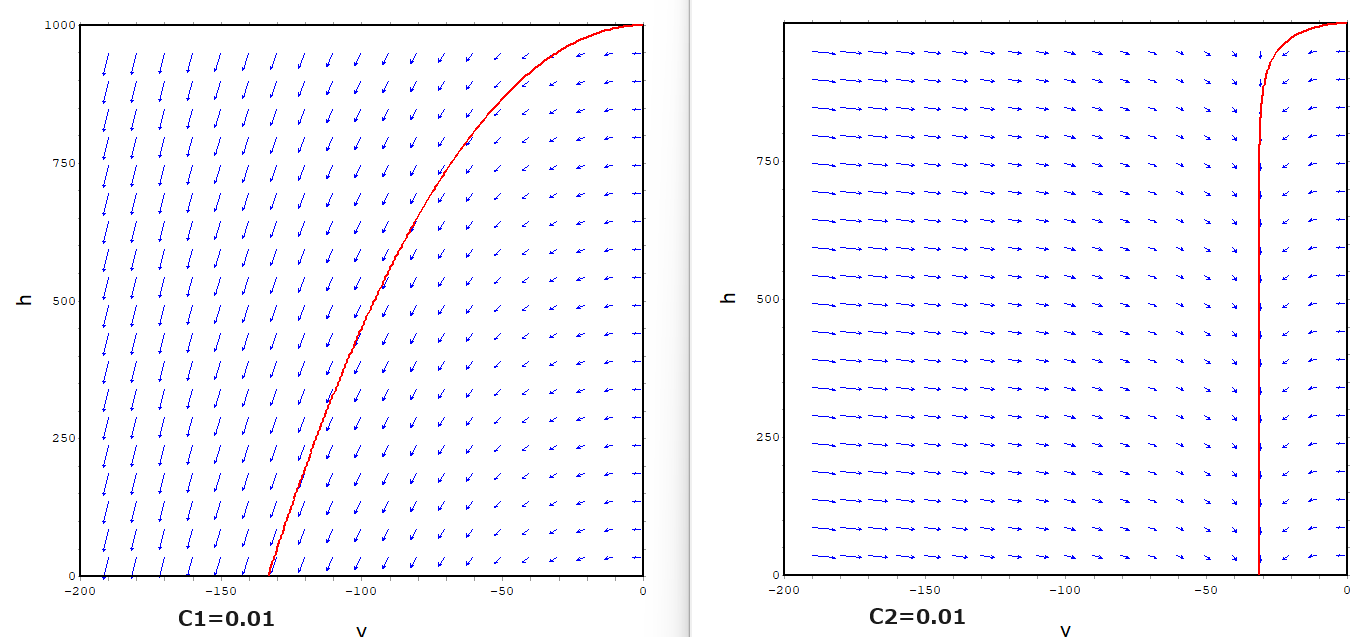
左の速度に比例の方では１０００ｍも落っこちているというのに今だ終端速度に達っせず。右の速度の二乗の方では１００ｍほど落ちる間にほぼほぼ終端速度に足しそのまま落ちていってます。
まあ、流体の中の物体なので、c2とかをそれらしく求めるのは大変ムツカシーと思いますけど、それっぽくplotdfすることはできると。ホントか？