ここ数回、plotdfパッケージを使わせていただいとります。しかしplotdfの真の御威光をアカラサマにするには、Phase plane(相平面)、phase portrait(相図)といった恐ろし気なものどもを避けて通るわけにはいかないようです。どうするんだ?そしたら本棚の奥からバッチリなご本が出てきたのよ。インド?
※「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
phase plane、phase portrait
地獄の底から蘇った古代の御本は、ベタなお名前の御本です。
DIFFERENTIAL EQUATIONS
米国の大学のGerorge F. Simmons先生が1972年に米国マグロウヒル社から出されたご本。初版からはすでに半世紀以上経過しております。しかし手元にあるます本は、
TATA McGRAW-HILL、New Delhi
出版のもの。元の米国版を在インドのマグロウヒルとタタ(インドの財閥のタタなのかね)の合弁と思われる会社で印刷したと思われるもの。なんでインド本?と思ったのだけれども、購入からも50年近く、忘却力の年寄にはその理由が思い出せませぬ。
まあともあれ、上記の御本には(ちゃんと読んでないから忘れてるのだけれど)微分方程式で書き表せる「システム」をphase plane(あるいはspaceというべきか)とphase portraitを使って解析する方法について語られております。
数学、物理学素人のお惚け老人がこの件について深く語りますまい。日本語のウエブ情報さがしても多数見つかります。一気にムツカシクなる傾向が強い中で、『デルタ先生の物理と数学の部屋』様の以下のページなどは分かり易いんでないかと。
振動・波動の基礎⑤-相平面について-単振動の場合 アニメーションで理解しよう
今回は、上記の教科書にごちゃまんと列挙されておる例題を拾いながら、相平面に表れる以下の典型的なものどもをplotdfを使って描いてまいりたいと思います。
-
- Centers、円や楕円を描いて回るもの
- Spirals、原点から、あるいは原点に向かってスパイラル状に動くもの(これの特殊なケースとして放射状の軌道のものもあり)
- Nodes、言葉に表しにくいっす。後の図を見てくれ、なもの。
- Saddle points、サドル型というべきか。詳しくは後の図を見てくれ、なもの。
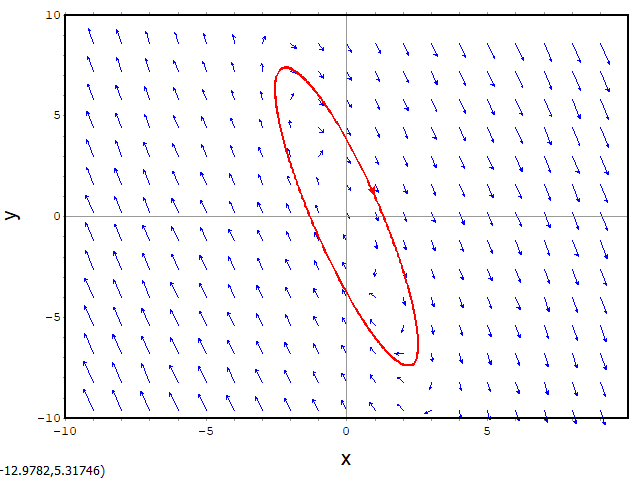
Centers
第152回の後ろの方で、減衰のない単振動をプロットしてます。このとき、位置zと速度vを軸にとって描きましたが、速度に質量をかければ運動量なので、速度vの軸は運動量とみなすこともできるっと。これぞまさに物理的な「相平面」の真髄?であります。
第152回では素直に「丸い」軌道を描いたので、今回はちょっと歪んだ軌道を描いてみます。
load("plotdf");
plotdf([5*x+2*y, -17*x-5*y],
[x, y],
[nsteps, 1000],
[trajectory_at,1,1],
[x, -10, 10],[y, -10, 10])$
描かれた軌跡が以下に。
Nodes
続いてはNodesと呼ばれている図形です。なんでNodeなのかはお惚け老人の知るところではありません。aをパラメータ化して変幻する図形としてみました。
plotdf([x, -x+a*y],
[x, y],
[parameters,"a=1"],
[nsteps, 1000],
[sliders,"a=-1:1"],
[trajectory_at,5,5],
[x, -10, 10],[y, -10, 10])$
テキトーに始点をばらまいて軌跡を描いたところが以下に。a=1のときね。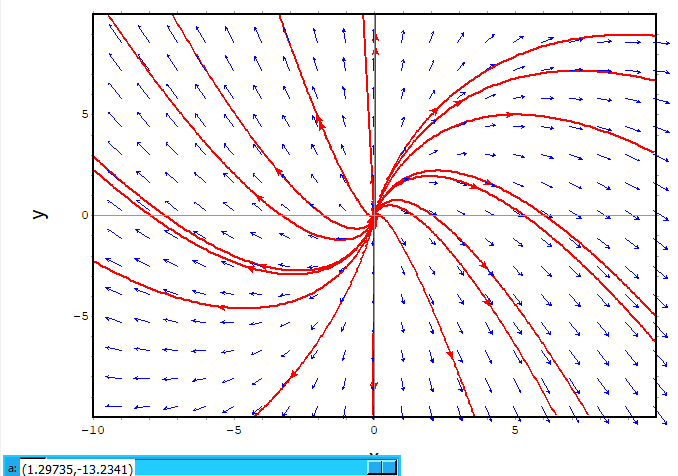
明らかに次に出てくるスパイラルとは違うね。
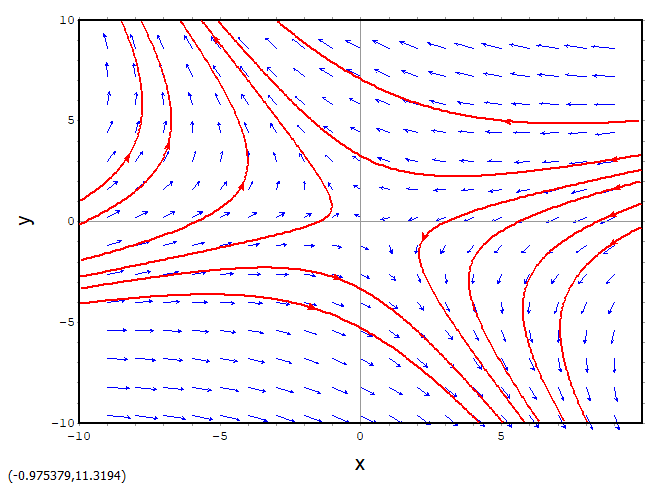
Spirals
お待ちかね、Spiralsです。
plotdf([a*x-y, x+a*y],
[x, y],
[parameters,"a=-0.5"],
[nsteps, 1000],
[sliders,"a=-1:1"],
[trajectory_at,5,5],
[x, -10, 10],[y, -10, 10])$
これまたaをパラメータ化してあるので、変化させると面白いです。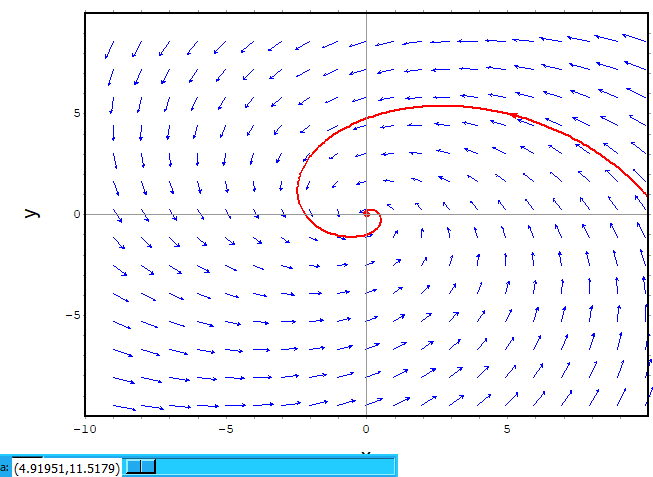
上記ではaはマイナスなので原点に向かって「落ちていく」感じっすけど、プラスにすると外へ飛び出す方向になります。
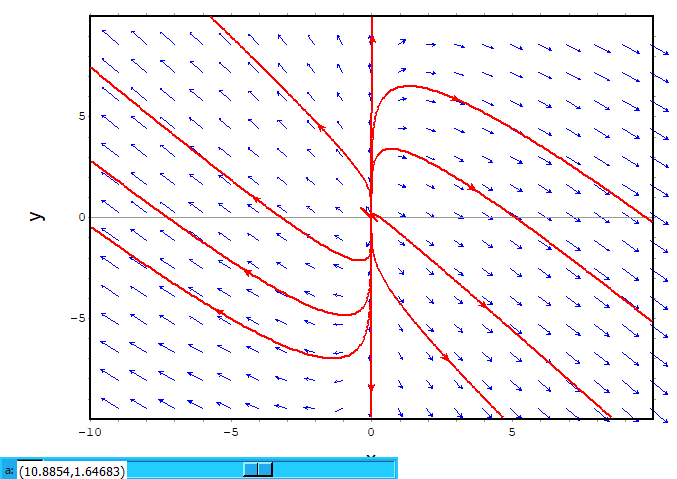
Saddle points
サドルポイントは分かりずらいので、ともかく軌跡をテキトーにちりばめてみてます。まずはplotdfのコードから
plotdf([-3*x-4*y, -2*x+3*y],
[x, y],
[nsteps, 1000],
[trajectory_at,5,5],
[x, -10, 10],[y, -10, 10])$
おまけ
Spiralsの特殊ケース? おまけは原点へ一直線のやつらです。お名前はついてないのだろうか?
plotdf([a*x, a*y],
[x, y],
[parameters,"a=-0.5"],
[nsteps, 1000],
[sliders,"a=-1:1"],
[trajectory_at,5,5],
[x, -10, 10],[y, -10, 10])$
グラフは以下に、やはりパラメータaを+にすれば外へ飛び出す方向に変わります。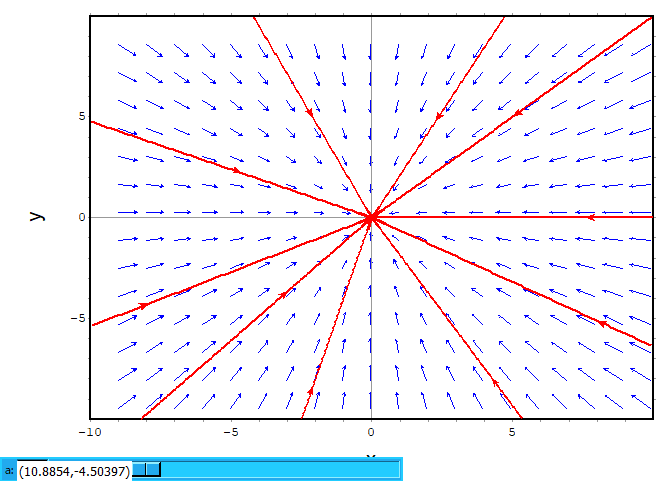
わけもわからずplotdf三昧という感じでしたな。