別シリーズで「∫」記号を頂くブロックどもが活躍。Pharoでも積分してみることにいたしました。こちらでは「何の工夫もないベタな数値積分」です。工夫はないですが、ターゲット関数を差し替えればいろいろできるハズ。なお下書きにしたのはRust言語で書いた短いコードです。Pharoで書いても短いです。
※Pharo関係記事の投稿順Indexは こちら
※Smalltalkの法灯を継ぐモダンな処理系Pharo様を練習してます。今回の動作確認には、Windows11上のWSL2の上のUbuntu24.04LTS上のPharo 10.0.0を使用しています。
下書きにしたRust版
以下の過去回のRust言語で書かれたソースを下書きにPharo様に移植してます。
RustにいればRustに従え(1) ∫[0:1] 1/(1+x^2)dx をRustで解く
Rust言語版では、mut(ミュータブル、書き変え可能）とか for とかを使わないという制限で積分をやっつけてます。今回のPharo様移植ではそのような縛りは全然気にしてないっす。お楽。
なお、積分対象の関数は 1/(1+x^2) でなくても処理できるように「一応」なってます。1/(1+x^2) の場合、積分区間０から１まで積分するとその答えはπ/4となることが分かっています。４倍するだけでπ（パイ、円周率）に近い数字が求まるので解答のチェックがやりやすいデス。
まずは結果から
今回練習用に作った MyIntegrator クラスを作製後、以下のようにして実行した結果が以下に。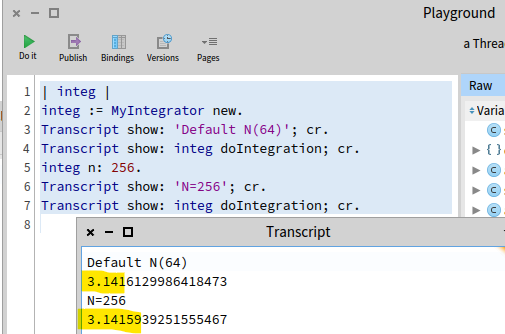
デフォルトの６４区間に分割で、3.141まで一致、２５６区間に分割すると3.14159まで一致しました。まあ計算はできてそうだな。
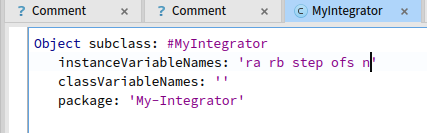
MyIntegratorクラス
まずはクラス定義。
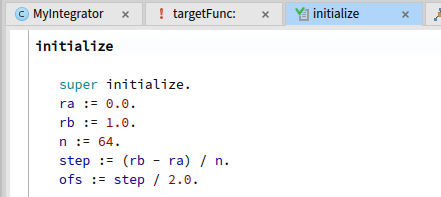
積分区間の下限がra、上限がrb、積分区間を n 分割して積分する区分数が n です。stepとofsは初期化時に ra, rb, n から計算して求めてます。
インスタンスの初期化メソッドが以下に。
今回のターゲット関数はデフォルト値のままでも積分が求まりますが、ra、rb、nを再初期化するメソッドは用意してあります。
さて、積分対象の「関数」は以下のような形でメソッドとして定義しておきます。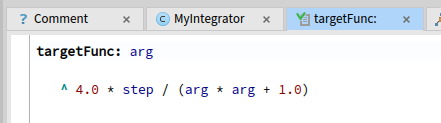
引数 arg が関数に与えられる独立変数値なので、それを使ってそのときの関数値を求めます。ミソはその値にインスタンス変数 step（積分する幅）を乗じたものを返すようにしてあることです。これで単純な短冊型で面積が求まりますな。
この関数を再定義すれば、ひねくれた関数でなければ積分できるでしょう。ホントか？
実際に積分を行う doIntegrationメソッドが以下に。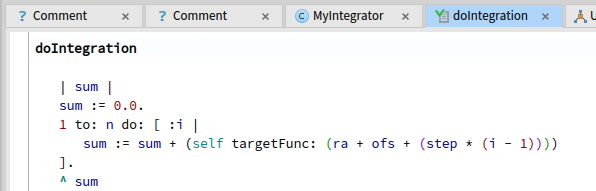
元のRustコードと比べると、書き変え(mut)する積算変数 sum など使っているのでカッコ悪い気がしないでもないです。まあPharo様は気にしないみたいだしお楽が一番。
細かいアクセサなど除き、以上で積分できるっと。