前回は「カオスからフラクタル図形を紡ぎだす」chaosgame関数の代表例ということで正三角形をランダムに動かしながらシェルピンスキーのガスケットが描かれるのを眺めました。でもシェルピンスキーだけじゃないです。４角形でも５角形でも６角形でもカオスゲームは成り立つみたいです。ただし数字の選び方がビミョ～。
※「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
chaosgame関数
以下のThe dynamics packageのドキュメント（日本語）でも掲げられているExampleは、シェルピンスキーのガスケット（有限回打ち切りなので近似形だけれども）です。
カオスゲーム（漫画でない方）を検索すると必ずシェエルピンスキー様が登場。それ以外の例はないのと思って検索したら、見つかったのが以下のページです。
https://mathworld.wolfram.com/ChaosGame.html
「数学の権化」のWolfram様のページです。そういえばお惚け老人も自分のスマホにWolfram Alpha（有料）をインストールしてあるのです。活用しているとはとても言えんな。。。実際、Wolfram Alphaにお伺いをたてればフラクタル図形が紡ぎだされる例が列挙されます。灯台下暗しならぬ、ポケットに解答。
さてパラメータさえ選べば、３角だけでなく、いろいろな図形からフラクタルすることができます。
４角形
３角の次は４角ということで４角形です。
chaosgame([[0, 0], [1, 0], [1, 1], [0, 1]], [0.1, 0.1], 2/5, 30000, [style, dots]);
このときの図形が以下に。４角形は地味ですがフラクタル（３００００回打ち切りなので近似形だけれども）してますぞ。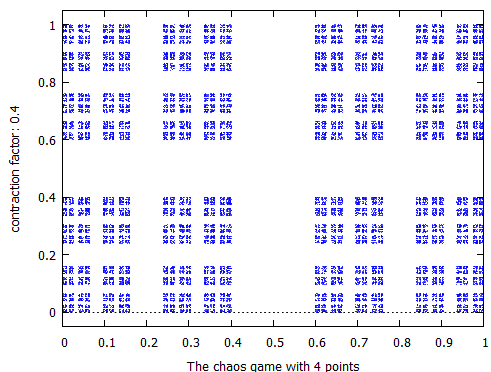
上記ではcontraction factorが 2/5 でしたが、contraction factorを 1/2にしてみるとその様相はまったく異なります。
chaosgame([[0, 0], [1, 0], [1, 1], [0, 1]], [0.1, 0.1], 1/2, 30000, [style, dots]);
シェエルピンスキーの時は 1/2 でうまく行ったのですが、４角形で1/2は以下のようなランダムな図形となります。
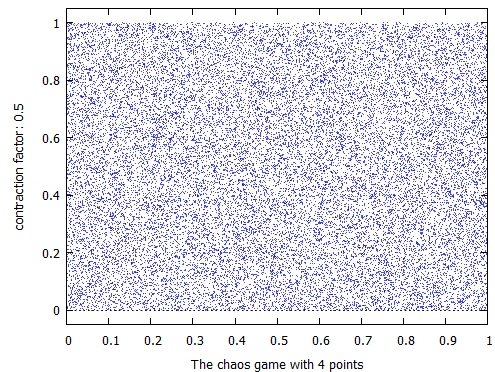
このねえ、うまく行くパラメータを最初に見つけた人は根気強かったのかな？
５角形
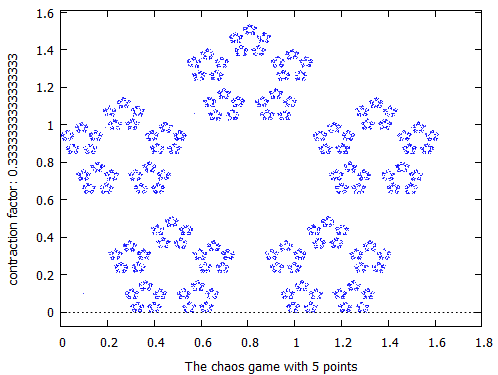
５角形を描くのに、頂点の座標を計算するのが辛かったお惚け老人です。５角形用のコードが以下に。
v1:[cos(2*%pi/5), 0]; v2:[cos(2*%pi/5)+1, 0]; v3:[2*cos(2*%pi/5)+1, sin(2*%pi/5)]; v4:[cos(2*%pi/5)+(1/2), sin(2*%pi/5)+sin(1*%pi/5)]; v5:[0, sin(2*%pi/5)]; chaosgame([v1, v2, v3, v4, v5], [0.1, 0.1], 1/3, 10000, [style, dots]);
この時の図形が以下に。
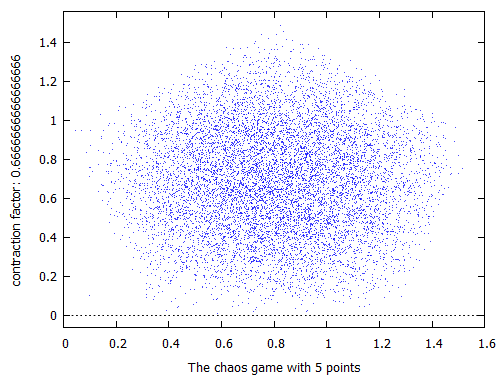
上記のcontraction factorは1/3でしたが、それを 2/3 に変えるとこんな感じっす。頂点を１回求めておけば後はお楽。
chaosgame([v1, v2, v3, v4, v5], [0.1, 0.1], 2/3, 10000, [style, dots]);
図形が以下に。2/3はダメなのね。。。
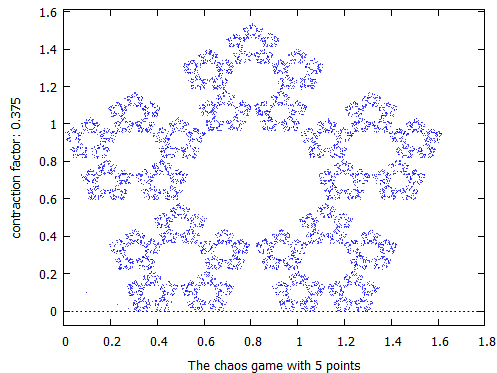
さらに、3/8だとこんな感じ。
chaosgame([v1, v2, v3, v4, v5], [0.1, 0.1], 3/8, 10000, [style, dots]);
これはフラクタル（有限回打ち切りなので近似。）
カオスゲーム、出来る気がしてきた？ ホントか？