
前回は連立漸化式の発展を観察。今回は反復関数系です。IFS: Iterated Function System。2次元の点をこねくり回す?のだけれども、chaos game同様、そこにランダムな介入があると。そんな乱数な?といってあら不思議。繰り返していくと何やら図形が見えてきます。その代表がバーンズリー先生のシダね。
※「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
IFS: Iterated Function System
さて、例によってifs関数のマニュアルページ(日本語)が以下に。
https://flex.phys.tohoku.ac.jp/texi/maxima-ja/maxima_54.html
反復関数系法ということで ifs関数がとりあげられております。引数はこんな感じ。さらっと書かれてもな~という取りつき難い感じです。
ifs ([r1, …, rm], [A1,…, Am], [[x1, y1], …, [xm, ym]], [x0, y0], n, options, …);
これを理解するには、中高生のころに学んだアフィン変換を思い出さずにはいられませぬ。2次元の場合ね。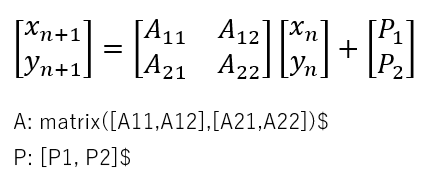
(Xn, Yn)なる点が上記の変換により(Xn+1、Yn+1)なる点に変換されます。行列Aが回転と拡大縮小、Pが並行移動を担うってか。そして、Maxima様的には上の行列で書かれた関係をその下のmatrix定義とベクトルを使って表記することが可能であります。
これを見てからifs関数のプロット例の定番中の定番、バーンズリーのシダのMaximaコードをご覧ください。
a1: matrix([0.85,0.04],[-0.04,0.85])$ a2: matrix([0.2,-0.26],[0.23,0.22])$ a3: matrix([-0.15,0.28],[0.26,0.24])$ a4: matrix([0,0],[0,0.16])$ p1: [0,1.6]$ p2: [0,1.6]$ p3: [0,0.44]$ p4: [0,0]$ w: [85,92,99,100]$ ifs(w, [a1,a2,a3,a4], [p1,p2,p3,p4], [5,0], 50000, [style,dots]);
なんだ、上の方の8行は4組のアフィン変換の準備じゃん。アフィン変換4つは分かったけれども、wという数字ベクトルは何だ?
ここで、4つのアフィン変換をmatrix定義のa1~a4のお名前で呼ぶことにすると、それぞれのアフィン変換を通過させる確率(積算だけれども)のリストがwです。
-
- a1 は 85%
- a2 は 92-85=7%
- a3 は 99-92=7%
- a4 は 100-99=1%
そして(x, y)の初期値が [5, 0]であり、50000回の変換を繰り返して、(x,y)組をプロットしていったものが以下です。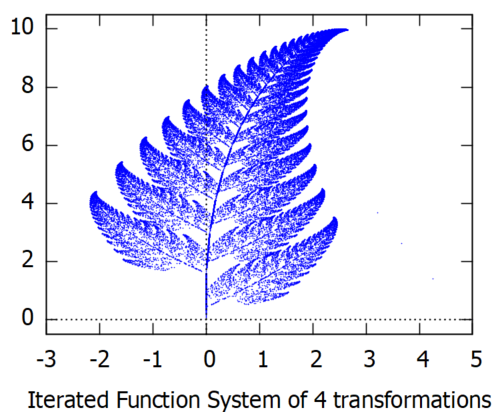
おお、フラクタルな。。。
当然、変換の係数とか、確率とか、式の本数とか「いじれる」場所は多々あるので、これを操作することで「別なシダ」類なども描けるみたい。やらんけど。
そんななか、『osawa-koki』様の以下のサイトで「各種のフラクタル代表選手」をいろいろパラメータを変えながらプロットできることに気づきました。あざ~す。
眺めているだけで飽きんよな。。。