前回まで dynamics パッケージの紡ぎだすカオスの中にフラクタルを観察してまいりました。しかし、dynamicsパッケージだけではなかったです。その名もズバリの fractals パッケージというものが存在。いままで見てきたようなフラクタル図形も描画できるけれども、ちょっと立ち位置が違うみたい?なんだそれ。
※「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
fractalsパッケージ
いつもお世話になっておりますMaximaの日本語マニュアルページが以下に。
こちらは以下のようにしてパッケージをロードしてから使い始めることになります。
load(fractals)$
三角(シェルピンスキーのガスケット、第158回)とか、シダの葉(バーンズリーのシダ、第164回)とか、マンデルブロ様(第157回)とか今まで見てきたような図形はみなこちらのパッケージにも該当関数が含まれております。
ただ同じフラクタルを扱うといってもスタンスの違いは引数に現れているような気がします(数学素人の老人の個人的な感想っす。)dynamicsパッケージは、その名のとおり、計算の過程に興味があるみたい。計算式を組み立てるところは自分でやらんとならないデス。メンドイ?でもま、いろいろ実験する余地が大いにあり。一方、今回の fractals パッケージはフラクタル図形そのものを「愛でている」感じがします。メンドイところは内部に包みこんで、繰り返し回数程度を所望の関数に与えれば即結果がでます。ただし、結果の提示の仕方には双方行き方が異なるみたい。設定メンドイdynamicsパッケージの方が図を描くところまで一気通貫で行ってくれるのに対し、 fractals パッケージはあくまでドットの位置を算出するところまで。図にするのは関数の外でplot2dに渡せちょうだい、という感じっす。まあ、どっちもドッチ?
既にdynamicsパッケージでやった図形を再度やってもトキメかないので、ここまでのところで出てこなかった図形を愛でてみたいと思います。
Koch雪片集合(コッホ曲線)
実はGo言語を使ってアンドロイドスマホ上で実験している別件シリーズの以下の回でコッホ曲線(一番簡単な奴だけれども)描いてます。
やっつけな日常(12) スマホでGo! 1.26186…次元から染み出すコッホ曲線
「有限の面積の中に納まる無限の長さの線」、1.26186…次元(フラクタル次元だけれども)であります。
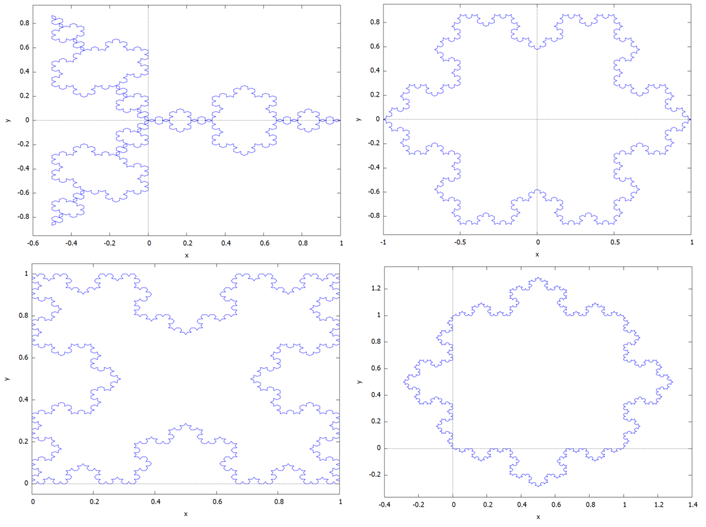
コッホ曲線と言えば雪の結晶みたいな図形が代表選手でないかと。Maxima様のマニュアルに例示されていた以下4例
plot2d([discrete, snowmap([1,exp(%i*%pi*2/3),exp(-%i*%pi*2/3),1],4)])$ plot2d([discrete, snowmap([1,exp(-%i*%pi*2/3),exp(%i*%pi*2/3),1],4)])$ plot2d([discrete, snowmap([0,1,1+%i,%i,0],4)])$ plot2d([discrete, snowmap([0,%i,1+%i,1,0],4)])$
ペアノ曲線、ヒルベルト曲線
空間充填曲線(space-filling curve)を最初に発見されたのがペアノ様で、ヒルベルト大先生も関わっておられるみたい。どこまでをペアノと呼び、どこからヒルベルトというのか数学素人老人はよく分かってません。3x3で分割したら(オリジナルの)ペアノ、2x2分割したらばヒルベルト?全部ひっくるめたらドッチ。なんじゃらほい。
しかし、この曲線(やっぱり簡単なやつだけれども)、以下の過去回にて練習してます。
やっつけな日常(15) スマホでGo!じゃない。ヒルベルト曲線
何気にGo言語をこのような目的に使っておったのね、自分。上記ではUbuntu上のGo言語で実習しているみたい。忘却力よ。
なお、fractals パッケージには以下のような恐ろし気な警告が書かれてます。マニュアル2か所から引用させていただきます。
警告: nと共に点の数は指数関数的に増加します。~(中略)~ もし 7以上なら Maximaはクラッシュするかもしれません。
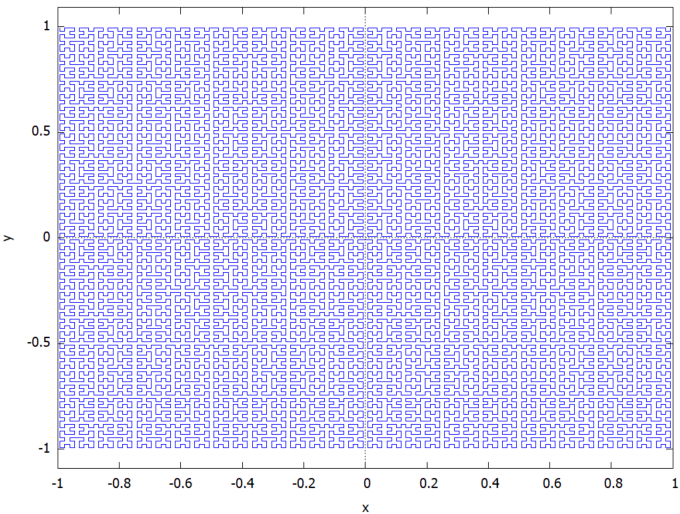
7は止めておいて、6でやってみた(根性無だな)結果が以下に。
plot2d([discrete,hilbertmap(6)])$
treefale関数
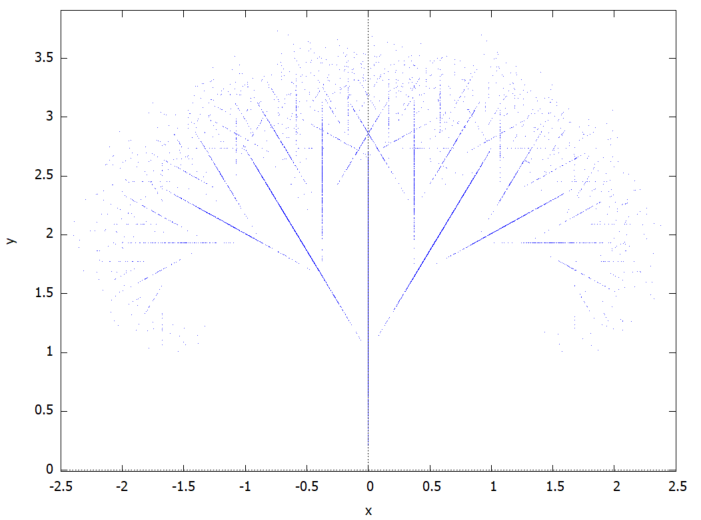
一瞬図形をみるとタートルグラフィクスで再帰で描いた図形にもみえますが、treefale関数は、内部に「確率的な選択」を擁している「反復関数系」みたいです。バーンズリーのシダと一緒ね。
plot2d([discrete,treefale(10000)], [style,dots])$
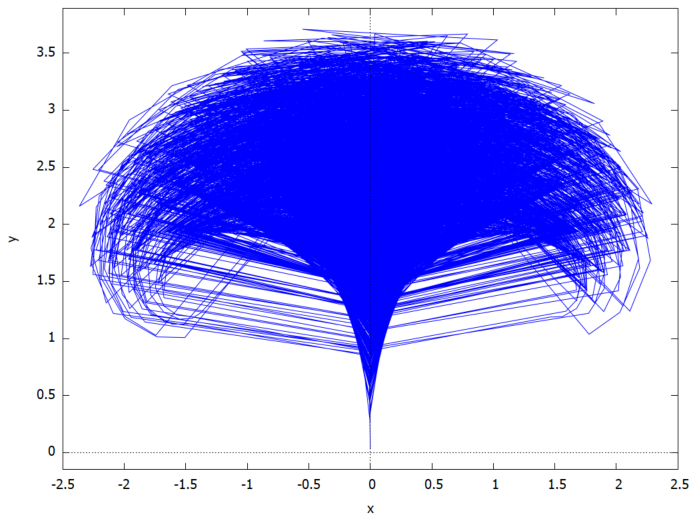
美しいのだけれども老眼では見難い図形っす。以下のようにしてえげつない感じにしてしまいました。
plot2d([discrete,treefale(10000)], [style,lines])$
確かに「確率的」な部分がそこここに見える感じ。しかし “fale” って何だ?南洋の壁の無い屋根だけのお家なのか。知らんけど。