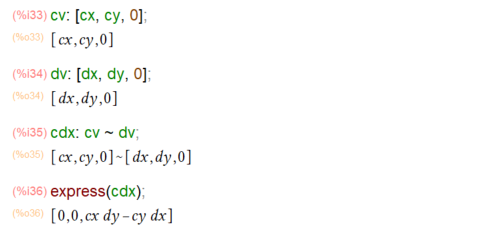過去回にて「ちょっと触って」みたものの、消化不良のまま打っちゃっていたパッケージに今回戻りたいと思います。vectパッケージとな。ベクトル解析用のパッケージです。このパッケージをば極めれば、グラディエントにダイバージェンス、カールにラプラシアンと昔苦しめられた記憶の者どもを自在に使役できるようになるのだとか?ホントか?
※「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- wxMaxima 22.04.0
- Maxima 5.46.0(x86_64-w64-mingw32)
- SBCL 2.2.2 (SBCL = Steel Bank Common Lisp )
vect パッケージ
ちらっと vect パッケージに入りかけた過去回が以下に。
忘却の微分方程式(30) ベクトル解析その1、MathematicaとMaxima
遥か昔のことゆえ、忘却力の老人はほぼ全てを忘れておるので、今回は、ほぼほぼ最初からやり直しです。トホホ。
なお、いつもお世話になっておりますMaxima様の日本語マニュアルページ(東北大様サイト内)の該当部分が以下に。
23. Matrices and Linear Algebra
さて今回は、パッケージのロードから始めないとなりませぬ。こんな感じ。
ロード直後に dimension などという変数の値を確かめてますが、これは「次元」です。3ということは、x、y、zの3次元てことでいいみたいです。zerovector()という関数を呼び出すと dimension で指定されている次元設定のときのゼロベクトルを返してくれるみたい。
vectパッケージの使い方、雲をつかむようなので、まずはデモを走らせてみます。
SHIFT+ENTERしつづけると、なにやら、分かったような分からぬようなデモが進捗します。デモ完了後に再び次元を拝見してみると、
2次元になってました。まあ、2次元で収まる話なら、2次元でやってしまう方がお楽。
ドット積、ここでは内積
ピリオド記号 . を演算子として使う「ドット積」というものあり。デフォルトの挙動に何も手を入れない状態では「内積」ということで良いみたいです。dimension: 2 の状態で2つベクトルを定義して内積求めたみたものが以下に。
どうもドット積は、ただ内積という理解では許してくれないみたいですが、今のところは大丈夫そう。。。
さて、内積につづき計算してみるのがグラディエントであります。これは「スカラー場」を入力にとって、その勾配のベクトルを返してくれるもの。2次元のスカラー量の「定義」をテキトーに放り込めば計算してくれるハズ。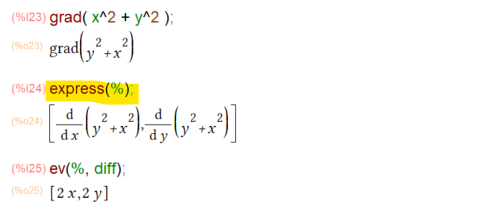
上記のように、gradにただスカラーを表す式を放り込んでも「grad」表示のままです。実際に偏微分の形に持ち込むには express() 関数にお願いする必要があるみたい。expressするとようやく微分の形(偏微分記号 ∂ を使ってくれないのが若干寂しいっす)になり、それを評価してやると微分結果が得られると。
~演算子、ここでは外積
チルダ記号 ~ を演算子として使う場合、ここでは外積ということでいいみたいです。ただし、テンソルにハマっていくと「ウエッジ積」というものに昇格するとかしないとか。知らんけど。
ともあれ、2次元空間では外積計算できるような気がしないので、次元を3次元に変更して外積を計算してみます。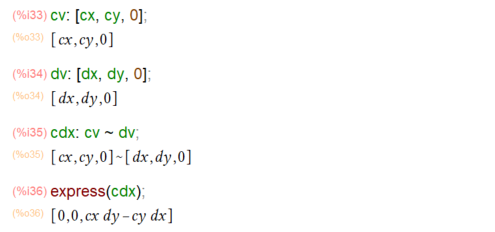
計算がお楽になるように、ベクトルcvとdvはxy平面内のベクトルとし、その二つの外積を求めたらば、ピタリz方向になるように仕組みましたです。内積のときはベクトルを . でつなぐだけで計算してくれたのですが、外積については、grad同様 express()関数の御出馬をお願いせんとなりません。
まあ、2次元もしくは3次元の空間内でベクトルの計算が出来るような気がしてきた。先は長そうだが。