前回、vectパッケージでgradient(勾配)の計算済。しかしプロットしてなかったです。今回はまず「スカラー場」の関数を定義してプロット、そしてそのスカラー場をgrad()関数に食わせてベクトルを計算、そしてベクトル場をプロットとな。ただしお惚け老人には3次元空間ベクトル場の表現はムツカシイので2次元ね。
※「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- wxMaxima 22.04.0
- Maxima 5.46.0(x86_64-w64-mingw32)
- SBCL 2.2.2 (SBCL = Steel Bank Common Lisp )
vect パッケージと plotdf パッケージ
今回は gradient を計算するのに vect パッケージを、またベクトル場をプロットするのに plotdf パッケージ(過去回で練習済)を使わせていただいております。
まず vect パッケージのマニュアルページが以下に
23. Matrices and Linear Algebra
つづいて plotdf パッケージです
https://maths.cnam.fr/Membres/wilk/MathMax/help/Maxima/maxima_68.html
gradient
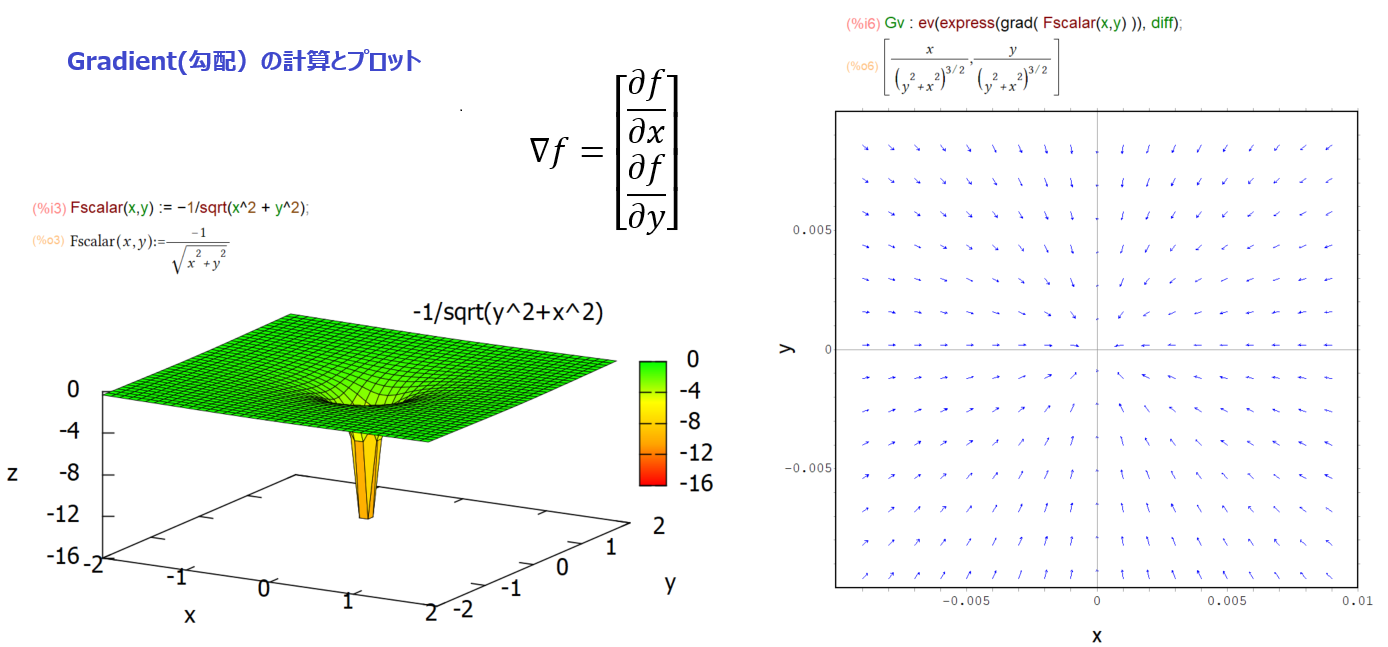
通常は3次元空間内で計算することになる gradient ですが、今回はプロットの都合で2次元です。関数f が2次元空間内でスカラー値を与える関数とした場合のgradが以下に。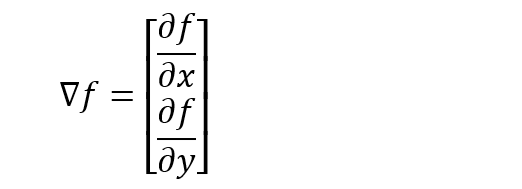
今回gradをとる関数
物理的な説明をすれば、距離に反比例するような何か?を表す関数であります。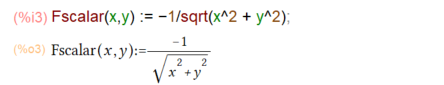
まずは上記をグラフにいたしとうございます。こんな感じでどうよ。
Fscalar(x,y) := -1/sqrt(x^2 + y^2); plot3d(Fscalar(x,y), [x, -2, 2], [y, -2, 2], [grid, 39, 39], [palette, [gradient, red, orange, yellow, green]], color_bar, [xtics, 1], [ytics, 1], [ztics, 4], [color_bar_tics, 4])$
上記によって関数の与えるスカラー値をzとしてxy2次元空間内にプロットした様子が以下に。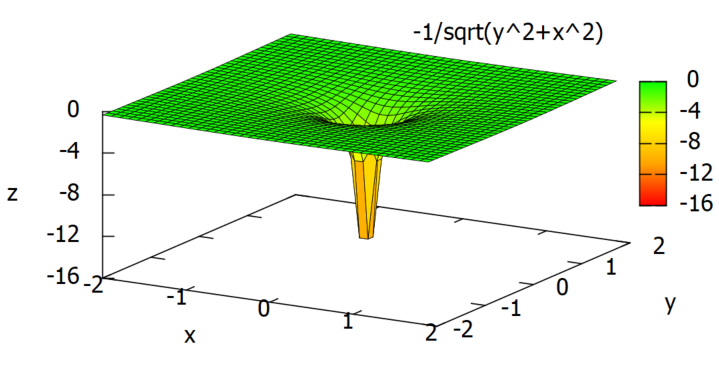
いかにも反比例な感じ?
gradを計算
さて、vectパッケージをロードし、上記のスカラー関数の grad をとってみたいと思います。
load ("vect");
dimension : 2;
Gv : ev(express(grad( Fscalar(x,y) )), diff);
デフォルトは3次元なので、ことさらに dimension:2 で指定をします。先ほど定義した関数を grad()に食わせた後、expressしてからevとちょっとメンドイですが、ここは前回やった通り。
gradient をとったらば、上記のようなベクトルになるみたい(本当に正しい結果かどうかは知らんけど。Maxima様の言う通りじゃ。)
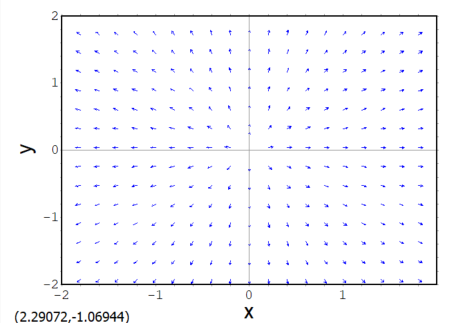
よっしゃーということで上記のベクトルを2次元空間内でプロットしてみます。
load ("plotdf");
plotdf(Gv, [x, -2, 2], [y, -2, 2]);
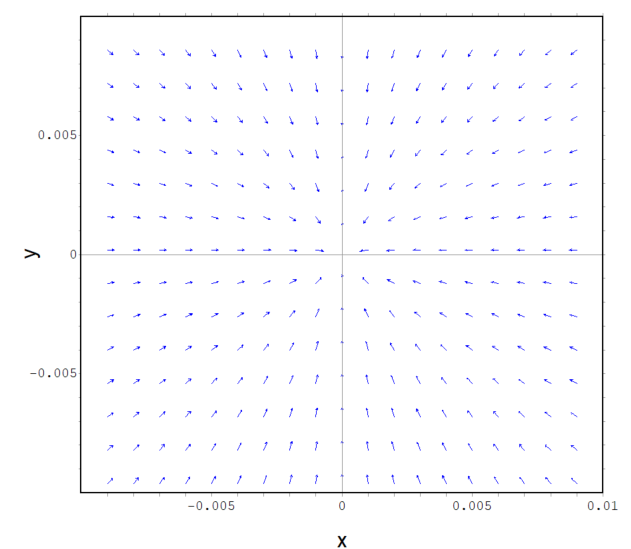
上記が、イマイチなのは、スカラー場で言うと、凹になった下の方から上に向かってベクトルの矢印が向かっているところ。常識にとらわれている老人としては上から下に「落ちる」感じの向きが自然っす。それに中心付近での集まり方が足らんな。修正したプロットコマンドが以下に。
plotdf(-Gv, [x, -0.01, 0.01], [y, -0.01, 0.01]);
ベクトル場のプロットっぽくはなったけれども、最初の3Dプロットの方が直観的で分かり易くね?プロットするだけだと grad とった意味ない?