
別シリーズ「ブロックを積みながら」にて、ブロック線図を描いてシミュレーションを行ってます。伝達関数が分かっていればブロック線図を描くのは自由自在、であるのです。しかし数学力の欠如した忘却力の老人には伝達関数を求めるのが辛いです、というかメンドクセー。でもMaxima様にお願いすればラプラス変換できたんだよね。
※「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- wxMaxima 22.04.0
- Maxima 5.46.0(x86_64-w64-mingw32)
- SBCL 2.2.2 (SBCL = Steel Bank Common Lisp )
やりたいこと
ホンワカした例で書くとヤリタイことは以下のようです。まずはシミュレーションしたい微分方程式系があると。以下はアリガチな力学的な振動モデルの例ですな。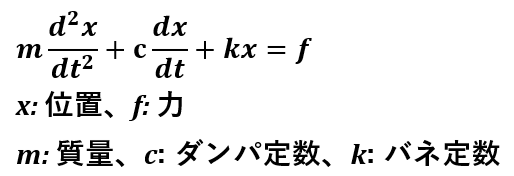
そして上記から、以下のようなブロック線図を描きて~ということであります。箱の中身こそ伝達関数ね。
ラプラス変換
さてMaxima様にお願して伝達関数をもとめる場合、そのものズバリなお名前の
laplace(expr, t, s)
という関数をつかうようです。時間 t 領域で記述された expr を s 領域に変換してくれる関数みたいです。忘却力の年寄りはラプラス変換の公式など覚えとりません(というか端から覚えてなかった。)laplace関数はそれらの適用を試みたのち、それでもダメだと2の矢(下請けのムズカシー関数)など呼び出してくれるみたいです。
なお、以下はラプラス変換の解説が含まれるMaximaのマニュアルページ(日本語、東北大様)へのリンクです。
ダメな問題の立て方
最初に悪い例として、ダメな微分方程式の立て方をやってみます。こんな感じ。
LT000: m*'diff(x,t,2)+c*'diff(x,t)+k*x=f; laplace(LT000, t, s);
上記のような微分方程式定義でも心の広い?ode2関数は受け入れてくれるかもですが、ラプラス変換する場合は、何が従属変数なのかハッキリさせとかないとうまく行きませぬ。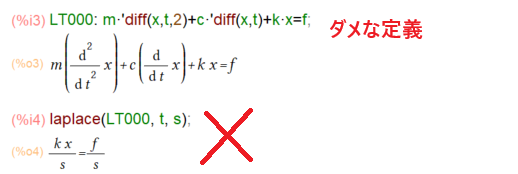
これでは上記のように何だかな~な結果に終わります。
マシな問題の立て方
ここでは、位置x や力f が時間 t の従属変数なのだということをハッキリさせときます。するとこんな感じ。
LT001: m*'diff(x(t),t,2)+c*'diff(x(t),t)+k*x(t)=f(t); LT002: laplace(LT001, t, s); LT003: solve(LT002, laplace(x(t),t,s));
lapace変換は、項毎に素のラプラス変換してくれるだけなので、
X(s)=伝達関数*F(s)
のような形に整理するためには、solveする必要があります。X(s)にあたるのがlaplace(x(t), t, s)みたいっす。
これで「一応は」変換できたことになりますが、やたら式の中に初期値が現れていてとっても見ずらいです。
初期値を与えた問題の立て方
上記のようにラプラス変換を実行後に、後から初期値をチマチマ与えていって見やすくする方法もありみたいですが、なんだか面倒だったので、以下では先にatvalue関数で初期条件を与えておいてからラプラス変換お願いしてます。
LT001: m*'diff(x(t),t,2)+c*'diff(x(t),t)+k*x(t)=f(t);
atvalue(x(t),t=0, 0);
atvalue('diff(x(t),t),t=0, 0);
LT002: laplace(LT001, t, s);
LT003: solve(LT002, laplace(x(t),t,s));
実行結果はこんな感じ。
ラプラス変換できたみたい。
「伝達関数」のとりだし?
まあ、上記で一応ラプラス変換できたみたいだけれども、ブロックダイアグラムの箱の中に書きこむ伝達関数のみを綺麗に取り出したいです。うまいやり方を思いつかなかったので、以下のようにしてみました。
LT004: 1/denom(rhs(LT003[1]));
これだね。

