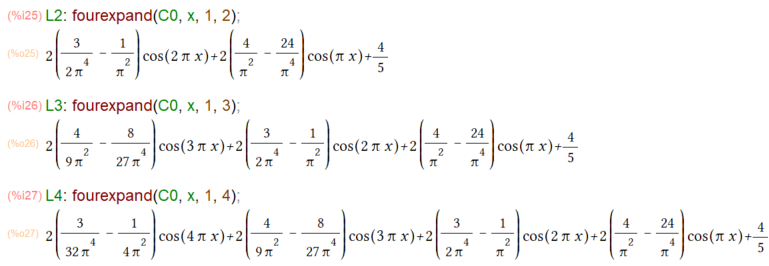前回はMaxima様にラプラス変換をお願いして伝達関数を求めました。今回お願いするのはフーリエ級数展開です。普段「高速フーリエ変換」とて数値的な解析にお世話になっておりますが、今回は数値ではなくシンボル計算で級数をもとめてみます。数学できない老人は間違えずに自力計算できる気がしません。でもMaximaで一撃よ。
※「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- wxMaxima 22.04.0
- Maxima 5.46.0(x86_64-w64-mingw32)
- SBCL 2.2.2 (SBCL = Steel Bank Common Lisp )
高速Fourier変換(数値計算)
本サイトでは「訳も分からず」高速Fourier変換(FFT)に頼ることシバシバであります。ざっとこんな感じ。
-
- LTspice回路シミュレータの周波数応答
- Digilent Analog Discovery2のWaveFormのスペクトルアナライザ機能
- Scilabのボード線図プロット
FFTのアルゴリズムなど自力で書ける気がしませんが、高速優秀なルーチンがそこここで実装されているのでお願いすればお楽。勿論、Maxima様にも数値計算の高速Fourier変換のパッケージは存在します。
fftパッケージ
しかしね、他のソフトウエアに実装されておるので、わざわざMaxima様にお願する必然性もないかな~という感じっす。
Fourier級数(シンボル計算)
さて、Maxima様の本領が発揮されるのが、
fourieパッケージ
ではないかと思います。各種関数のフーリエ級数を求めたりするための関数などが収められているパッケージです。使い方はいつもお世話になっております東北大様の以下のマニュアルページ(日本語)で。
28. Sums, Products, and Series
以下のようにパッケージをロードして使い始めます。
load("fourie");
フーリエ級数を求める
つべこべ言わず、関数を定義(以下ではf0という御名前です)して、fourier関数を呼び出せばフーリエ級数の係数をもとめてくれます。
f0(x) := 1-x^4; C0: fourier(f0(x), x, 1);
上記のfourier関数は「区間 [-1, 1]上で定義された f0(x)の Fourier係数のリスト」を返してくれます。勿論、区間は所望の幅に設定できます。
予想どおり、bnは0なのね。。。ちょっと簡単になって良かった。当たり前か。
さて教科書的なn=無限大までの級数を求めるには totalfourierという関数を使うと良いみたいです。
一方、特定の nまでで打ち切りの級数を求める場合、fourexpandという関数が使えます。以下は上のfourier関数で求めた係数C0を使って、n=2, 3, 4のケースを計算してみる場合。
L2: fourexpand(C0, x, 1, 2); L3: fourexpand(C0, x, 1, 3); L4: fourexpand(C0, x, 1, 4);
nが大きくなるにつれ、段々長くなっていきます。あったり前か。でも有限なのでこれは実際に数値にしてプロットして見れる筈。
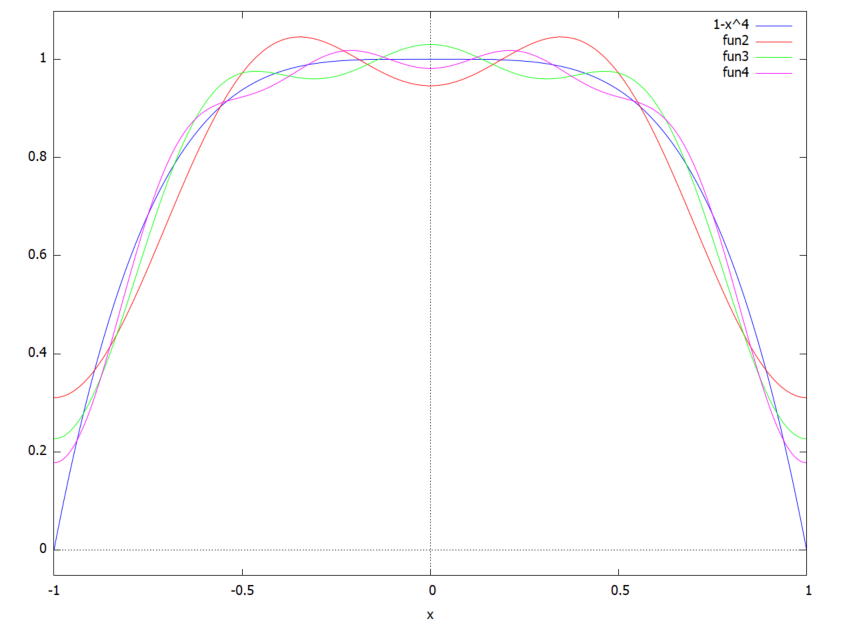
上記のL2、L3、L4をプロットしてみるコマンドが以下に。
plot2d([f0(x), L2, L3, L4], [x, -1, 1])
青色のお山が元の4次の式です。赤のfun2がL2の曲線、緑のfun3がL3の曲線。ピンクのfun4がL4です。nが増えるにしたがって青に肉薄?している感じが分かるっす。