
前回はMaximaで求めた伝達関数をScilab/Xcosに「輸入」し、その過渡応答の時間波形を観察してみました。しかし本シリーズの過去回では微分方程式を伝達関数化せず「ほぼほぼそのまま」小分けに積分するスタイルでも過渡応答波形をみています。まあね、同じ結果になる筈ではあるのだけれど、今回は2つのスタイルを比較。
※「ブロックを積みながら」投稿順 index はこちら
※動作確認にはWindows 11の パソコン(64bit)上にインストールしたScilabの以下バージョンを使用しています。
Scilab 2024.0.0
微分方程式を直接Xcosフローに落とし込む
過去回で、数学不得意老人は微分方程式をほぼほぼそのままXcosのフローに落とし込む形でシミュレーションを行ってます。「公式にあてはめるだけ」とはいえラプラス変換、自前で計算すると何か間違えそうなので遠慮?してきました。まあ、数式処理の人気者、Maxima様を使って伝達関数求められるのならば、それはそれ使えばハッピー?ホントか?
今回は以前からやっていた微分方程式「直接」方式を再度練習、前回の伝達関数方式と比較してみます。
念のため前回の微分方程式を再掲します。「ありがちな」バネーダンパ系で減衰振動するシンプルな力学モデルっす。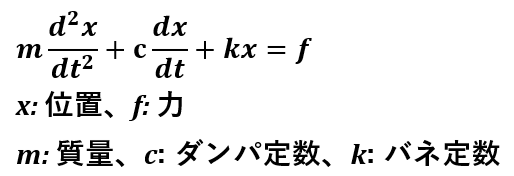
さて上記の微分方程式をXcos(Scicos)のフローにしたものが以下です。加速度 d^2x/dt^2を a、速度 dx/dtを v と表してます。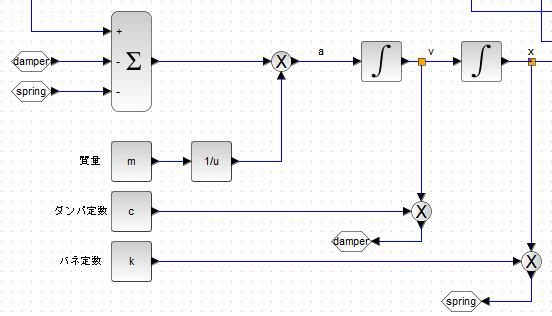
左上のΣのところが、ダンパとバネの力を移項した以下の部分です。
f – c*(dx/dt) -kx
その結果を質量mで割ってやれば加速度 a が求まり、加速度を積分すれば速度 v、速度を積分すれば位置 x が求まるという塩梅です。
これはこれで、淡々と置き換えていくだけなのでムツカシーことはなんにもないです。
今回シミュレーションのフロー
前回作成のフローで、伝達関数方式での過渡応答を求めるための、コンテキストの設定、力Fの波形の定義、シミュレーション設定などは既にできているので、それにそのまま相乗りする形で上記のフローと合体させてみました。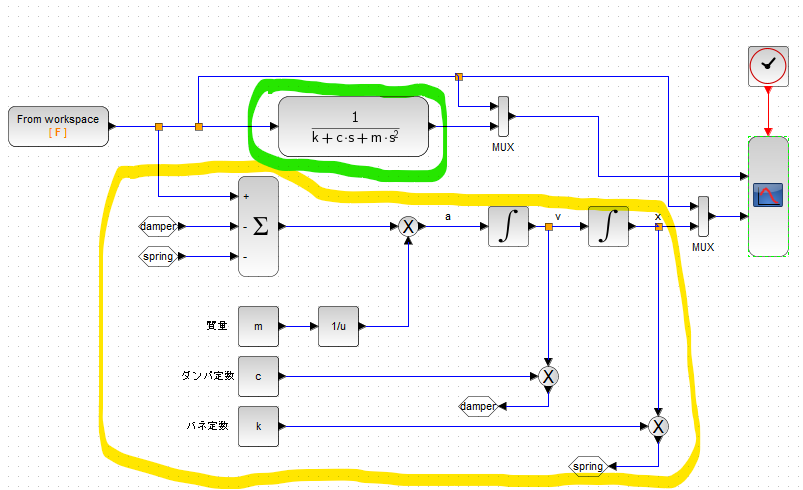
緑のマーカ部分が、前回の伝達関数ブロックです、シンプル。一方、黄色のマーカ部分が、今回の微分方程式そのまま方式?のブロックダイアグラムです。メンドクセーです。でも、加速度とか速度とか内部のう動きがモロミエなのでそれはそれで良いかも。
過渡応答を求めた結果
以下グラフの上側が「伝達関数」方式、下側が「微分方程式そのまま方式」の結果です。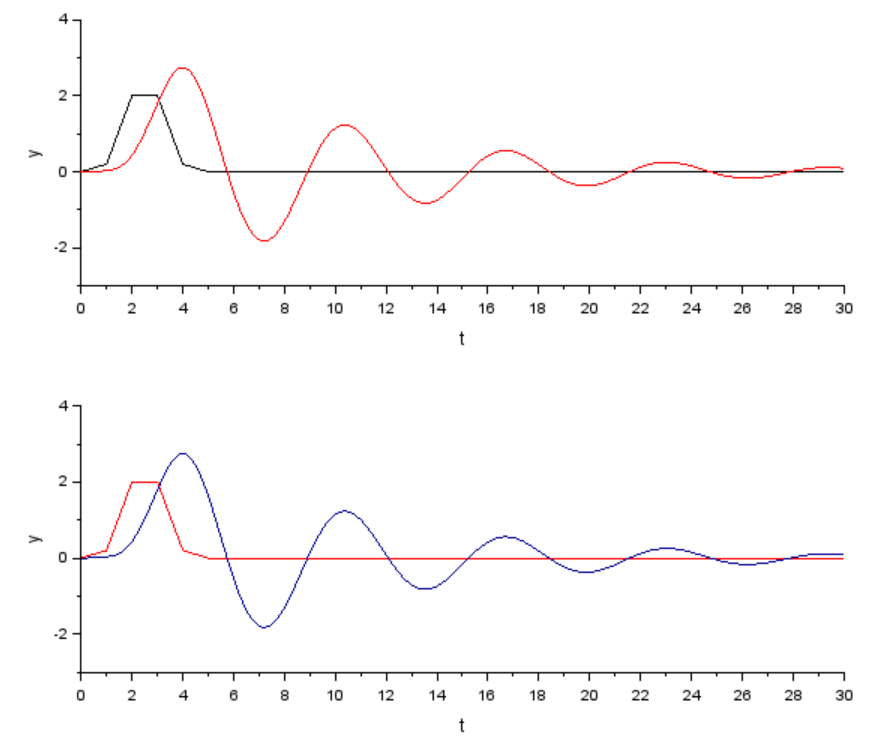
見ての通りで結果は一致しておるようです。まあ、当然なんだけれども。