前回は2次元画像用の周波数ドメインでのフィルタを設計するときに「お役立ち」らしいフィルタの可視化ツールを練習。今回は前回やらなかった、肝心の画像をフィルタするところをやってみます。フーリエ変換後フィルタでご所望の周波数帯を取り出してフーリエ逆変換で戻すというフツーの使い方。素人老人は全ステップ「可視化」して確認。OK?
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※Windows11上の Scilab2024.0.0およびScilab上のScilab IPCVツールボックスを使用させていただいております。
2次元画像用周波数ドメインフィルタ生成関数 mkfftfilter
さて、ながったらしいタイトルとなりましたが、画像に対するフィルタを生成してくれる関数が、mkfftfilter です。引数は4つ。
h = mkfftfilter(image,name,rc1,rc2)
-
- image、ソースとなる画像イメージ。ここから画像サイズを得る、多分。
- name、フィルタのお名前。gauss とか expとか文字列で与える。
- rc1、正規化されたカットオフ周波数その1
- rc2、正規化されたカットオフ周波数その2
今回使用してみた、gauss と butterworth1 フィルタの両方とも、カットオフ周波数は rc1のみ用いているみたいで、rc2は無くても動作しました。指定のフィルタ形式によっては rc2 を要求するものもあるみたいデス。
gauss、rc1=0.1
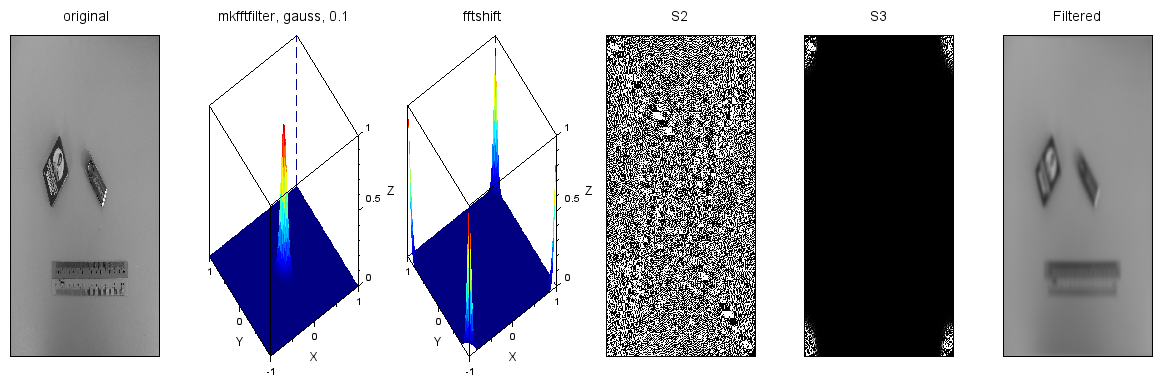
ヘルプファイルの処理例が上記のパラメータでやっていたので、そのときの様子をステップ・バイ・ステップで眺める処理が以下に。
S = imread(fullpath(getIPCVpath() + "/images/measure_gray.jpg"));
h = mkfftfilter(S,'gauss',0.1);
hS = fftshift(h);
S2 = fft2(im2double(S));
S3 = S2.*hS;
S4 = real(ifft(S3));
scf(0); clf;
subplot(161); title('original'); imshow(S);
subplot(162); title('mkfftfilter, gauss, 0.1'); imsmoothsurf(abs(h),100);
subplot(163); title('fftshift'); imsmoothsurf(abs(hS),100);
subplot(164); title('S2'); imshow(S2);
subplot(165); title('S3'); imshow(S3);
subplot(166); title('Filtered'); imshow(S4);
最左端がオリジナル画像、その次から mkfftfilterで生成したフィルタを可視化したもの。その生成フィルタをfftshift使って再配置したフィルタ(実際にはこれを使う)。砂をばらまいたようなS2が元画像のFFT2によるフーリエ変換の結果、S3はそれにフィルタをかけて「所望の部分を取り出したもの」、そして右端がフィルタ結果を逆フーリエ変換して画像に戻したものです。たしかに右端はボンヤリしておりますなあ。LPF。しかし、S3と右端を比べると周波数の端っこのほんのチョッピリだけ使っただけでここまで画像に戻るのかという感じがしないでもないです。ヒトの目は周波数低いところばかり見えとるのだと。
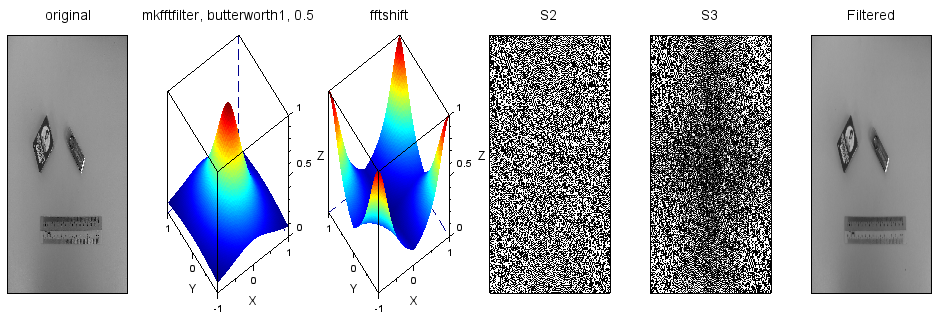
butterworth1、rc1=0.5
フィルタ形式を変更してみました。ついでにカットオフ周波数も大幅に上げてみました。実体処理では以下1行の変更です。
h = mkfftfilter(S,'butterworth1',0.5 );
フィルタの「可視化」からは最初の例からかなり「取り出す範囲」が変わっているのが分かるし、S3の周波数領域での画像も最初の例のベタ黒に近いものからはかなり細かくなってる感じがします。しかしフィルタ結果はさほど変わった気がしないね。コマケーところの表現は大変なのね。。。