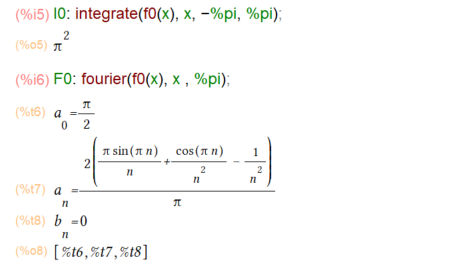前回は fourieパッケージを使ってフーリエ級数（シンボル計算）を求めてみました。でも何を一番フーリエ級数展開したいかといえば、ぶっちゃけ、三角波、方形波に正弦波の一部変形した波形など「ありがちな周期関数」です。電子系にありがち？今回は周期関数１周期分の波形をもってきてシンボル計算でフーリエ級数展開してみるべし、と。
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- wxMaxima 22.04.0
- Maxima 5.46.0(x86_64-w64-mingw32)
- SBCL 2.2.2 (SBCL = Steel Bank Common Lisp )
周期関数
fourieパッケージは、数値的な高速フーリエ変換ではなく、フーリエ級数をシンボル計算するためのパッケージです。以下のようにパッケージをロードして使い始めます。
load("fourie");
今回は、以下の２つの周期関数の１周期分（周期は２πとします）をとってきて、そいつらをフーリエ級数展開してみたいと思います。
-
- 三角波
- 方形波
三角波
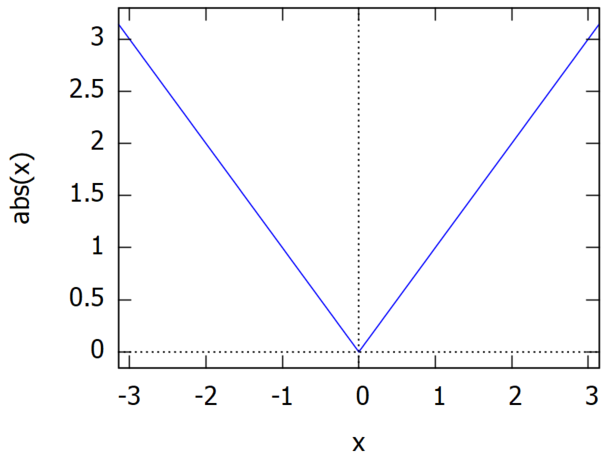
Maxima上で三角波を定義するのに用いたのは絶対値関数 abs です。これをフーリエ級数展開するターゲット関数 f0(x) として定義してプロットしてみます。
f0(x):=abs(x); plot2d(f0(x), [x, -%pi, %pi]);
プロット結果は以下に。
上記の２π周期で繰り返される波形をxの左右に繋ぎあわせていけばお馴染みの三角波が得られる筈。
ただ上記の絶対値関数、連続だけれど、ｘ＝０でかくっと折れ曲がっているのでそこでの微分は不可の筈。でも積分もできれば、フーリエ級数展開の係数も求めることが可能。
I0: integrate(f0(x), x, -%pi, %pi); F0: fourier(f0(x), x , %pi);
上記の結果が以下に。
ちゃんとフーリエ級数の係数求まっているみたいです。グラフを見ないでも一目瞭然なことに「偶関数」です。n=2と、n=4のときの展開の結果を元の関数に重ねてプロットする処理が以下に。
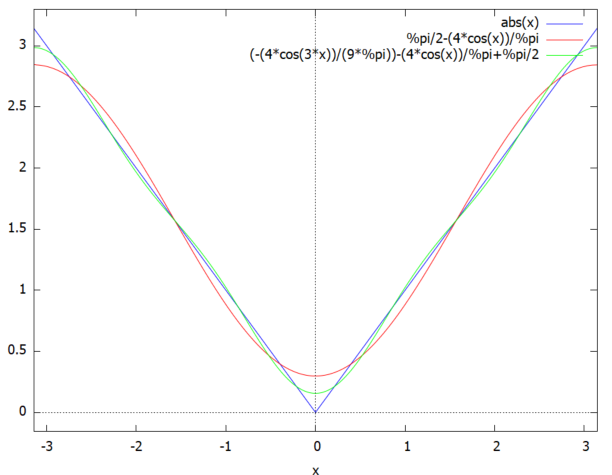
L02: fourexpand(F0, x, %pi, 2); L04: fourexpand(F0, x, %pi, 4); plot2d([f0(x), L02, L04], [x, -%pi, %pi]);
そのプロット結果が以下に。
n=4くらいでも結構雰囲気でてるじゃん。ホントか？
方形波
さて、方形波を定義するのに使ってみたのは、signum関数(数学的な表記としてはsgn関数）です。
f1(x):=signum(x); plot2d(f1(x), [x, -%pi, %pi]);
そのプロットが以下に。
これをやはり左右に繰り返していけば、みなれた方形波（この場合はオフセット０，振幅１のデューティ50%)が得られる筈。
fourieパッケージのfourier関数を適用して係数を求めることは可能。奇関数であるので、a_0, a_nは０であることは明らか。
ただし、上記ではb_nを表すのに、signumが残ってしまってます。このままだと、以降のフーリエ級数展開は上手くいきませなんだ。やっぱりx=0のところに0がいて、ここで不連続があるのがマズイ？
そこでx=0のところのsignumの定義をみなかったことにしてチョロまかし、 b_n を自前で計算してみることに。大丈夫か？まあ計算するのはMaxima様だけれども。
BN_x: (2/%pi)*'integrate(sin(n*x), x, 0, %pi); BN_y: ev(BN_x, nouns); BN: foursimp(BN_y); F1: [a[0]=0, a[n]=0, b[n]=foursimp(BN)];
結果が以下に。b_n らしきものが求まったあと、fourieパッケージのfoursimp関数にお願いすると「それらしい」形が求まりました。
上記の末尾では「手動にて」フーリエ係数のリストを作成してます。この設定ができれば、fourexpand関数などを適用可能になる筈。
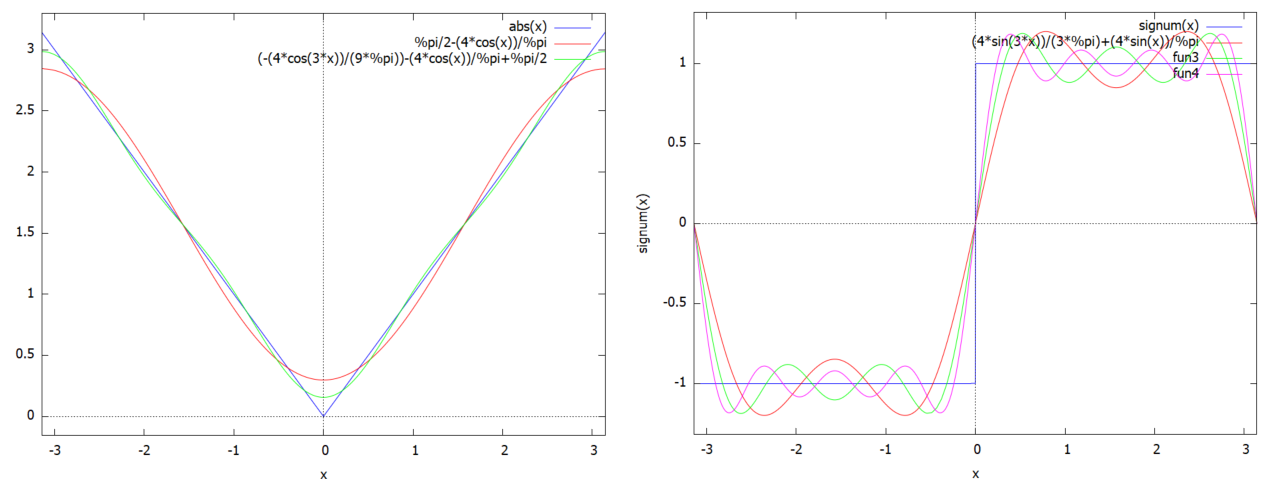
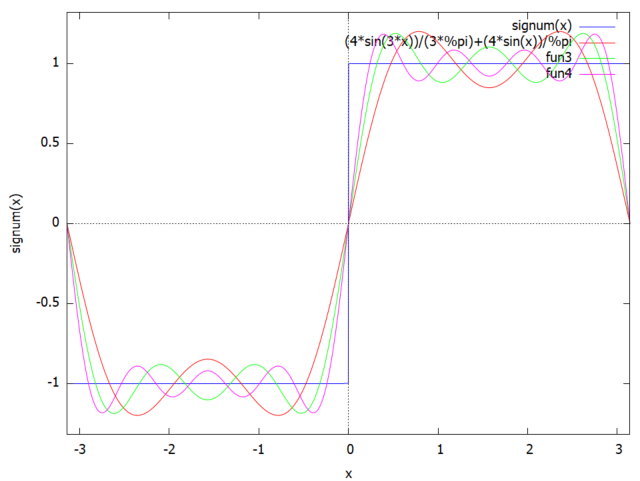
適用してみます。今回は奇関数なので、n=3、5、7まで展開したものを元関数と重ねてプロットしてみました。
L13: fourexpand(F1, x, %pi, 3); L15: fourexpand(F1, x, %pi, 5); L17: fourexpand(F1, x, %pi, 7); plot2d([f1(x), L13, L15, L17], [x, -%pi, %pi]);
その様子が以下に。
プロット結果が以下に。
なんだかんだいって、近づこうと努力はしているみたい。。。ホントか？