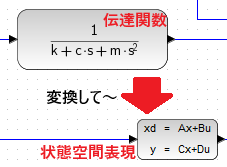
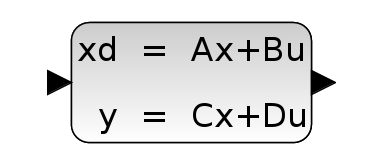前回は、微分方程式から求めた伝達関数表現をシミュレーションする方法と、微分方程式「そのもの」の要素を小まめ?にブロック表現して繋ぎ合わせる方法で結果が一致することを見ました。今回は状態空間表現しても結果が一致するところを確認してみます。でも状態空間表現、求めるのはどしたら良いの?伝達関数から変換一撃。
※「ブロックを積みながら」投稿順 index はこちら
※動作確認にはWindows 11の パソコン(64bit)上にインストールしたScilabの以下バージョンを使用しています。
Scilab 2024.0.0
CLSS(Continuous stat-space system)
前回確認した2つの方法よりも、「状態空間」で表現する方法の方がモダーンで後の展開が期待できる、ような感じがします。先々楽しみ?現代的な制御はこちらかね。さて微分方程式まで立ち戻って状態空間表現の行列やらベクトルやらを再構成しても良いのですが(でもメンドイっす)、伝達関数が既知なのであれば、伝達関数から変換して求めることが可能らしいです。
Scilabには tf2ss (transfer function 2 stat-space ということだとおもいます)という名の変換関数があり、伝達関数を与えると、状態空間を表現する syslin リストというオブジェクトを返してくれます。このオブジェクトの中に状態空間表現のA、B、C、Dと呼ばれる行列(ベクトル)どもも含まれてます。そしてこれを個別に取り出してくれる関数として abcd というそのものズバリのお名前の関数があります。
今回の「ダンパ付きのバネ振動系」の伝達関数をABCDに自動変換する操作が以下に。
s=poly(0,'s'); m=1; c=0.25; k=1; sl = tf2ss(1/(k + c*s + m*s^2)); [A,B,C,D] = abcd(sl);
伝達関数を記述するのに使うラプラス演算子 s は「素の」Scilab上では、%sと記すことになってますが、最初の s=poly(0, ‘s’)という御まじないにより、%なしのsで記述できます。%と記号の有無はお好みでってことかい。ABCDは実数の行列(ベクトル)なので、伝達関数の中で使っている定数には具体的な値を入れとかねばなりませぬ。m(質量)、c(ダンパ定数)、k(バネ定数)にはXcos(Scicos)シミュレーションのときと同じ値を代入しておきましたぞ。
上記操作の後、Scilab上で、ABCDを調べてみるとこんな感じ。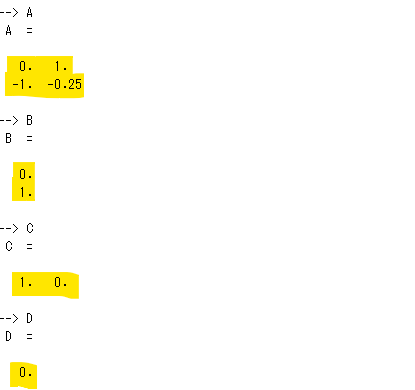
上記のようにABCDが求まってしまえば、後はXcos(Scicos)にCLSSブロックを配置し、その中のABCDに上記の値を代入すれば連続時間の線形状態空間の定義は完了っす。フローが以下に。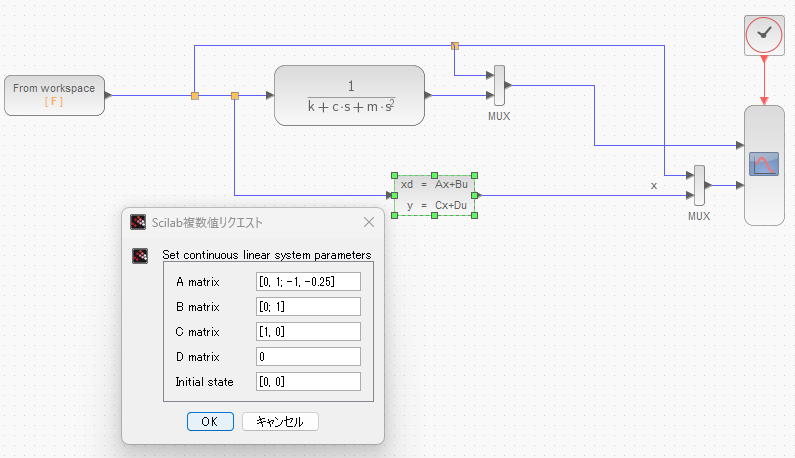
シミュレーション
もともとの伝達関数から求めた状態空間の表現なので、異なる挙動が出てきたらビックリですが、一応、並べてある2つをシミュレーションして結果を観察してみます。こんな感じ。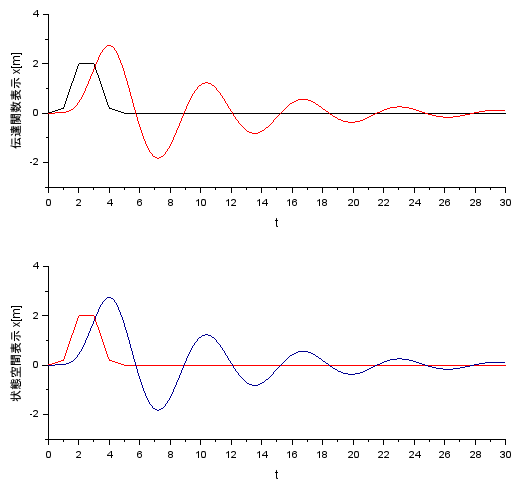
伝達関数表現と状態空間表現の両方で同じ結果が得られたみたい。平穏無事でよかった。