Maximaに関しては先達の方々が非常に多数の日本語解説ドキュメントを公開しておられます。ありがたい限り。しかし立派な文書が多過ぎて見逃していたものがあったことに最近気づきました。溝口純敏様著「Maxima を使った物理数学基礎演習ノート」であります。まさに老人が練習したかったことをまとめてくださっているPDFです。
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- wxMaxima 22.04.0
- Maxima 5.46.0(x86_64-w64-mingw32)
- SBCL 2.2.2 (SBCL = Steel Bank Common Lisp )
Maxima を使った物理数学基礎演習ノート
手元のバージョンで全６２４ページになる溝口純敏様著のドキュメントの在処は以下に。
http://www9.plala.or.jp/prac-maxima/
手元でダウンロードして拝見させていただいてますバージョンは以下です。
令和4 年3 月 第八回改訂
以下「Maxima を使った物理数学基礎演習ノート」を指すばあい「ノート」とのみ記させていただきます。さて「ノート」「第１章はじめに」から１か所引用させていただきます。
数式の展開に多くの時間をかけるのでなく、Maxima などの数式処理システムを使って物理数学を学ぶのが効率的な学び方ではないかと思い、本書をまとめました。
いやあ、そういうご本が欲しかったデス。
初期設定の件
いつも使っているwxMaximaをつかって問題なく演習などできそうではあるのですが、「ノート」の末尾の方、
A.1 wxMaxima を使用した演習の進め方
という付録があります。そこをまず読ませていただきました。そこでは適当なテキスト・エディタで「Maximaへの入力を書いてコピペ」という方法を推奨されています。お惚け老人もかねて行ってきた方法なので、これは今までどおりで良いなとほくそ笑みましたです。
１件、お惚け老人が見落としていたことに、CTRL＋ENTERの件がありました。入力した式を評価してもらうのはデフォルトのままCTRL＋ENTERで行ってきたのですが、wxMaximaの設定によっては、ENTERで評価することもできたのですね。知らんかったよ。上記付録にかかれていたので、改めてwxMaximaの「設定」みたら以下にありました。下の方だったので見落としていたね。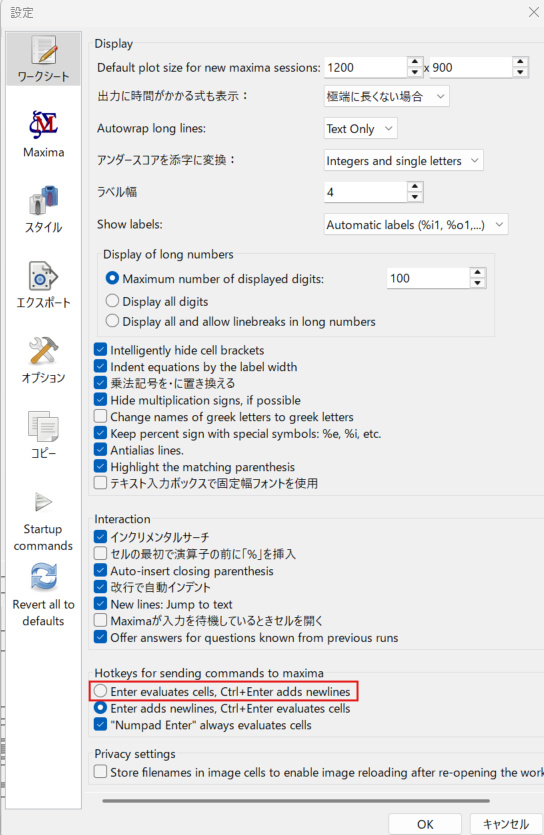
いや～、wxMaximaを使い始めたころに知っていたらきっとENTERで即評価に設定したですけど、CTRL＋ENTERに慣れてしまった今となっては変えられませぬ。手が覚えている。ホントか？ 折角のおすすめにも関わらず。
もう１件、MaximaからLatex形式の式を取り出せる件、選択してからの右クリック・メニューですな。このPDF自体がそれにもとづき「LATEX2ε」を駆使されて作成されたもののようです。当方、LATEX必要になると苦し紛れにインストール不要なWeb上のツールでお茶を濁してました。しかし、本PDFの演習をやっていくとそのうちLatexしたくなるような複雑な数式がバンバン登場しそうです。後でスタンドアロンで使用できるようにしないと。。。まあ、今回はいいか。
第２章 微分・積分から2.1 微分
２．１の最初は、左辺に微分を行うdiff関数のクオート、名詞形、スンドメ形？を置き、右辺にクオートを外して、その評価結果を置くという形で多数の関数の微分を列挙してます。１例引用するとこんな感じ。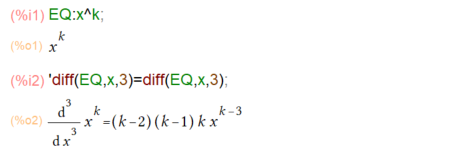
まあ、フツーの微分については、今までも散々やってきたので、全部やらんでも、いいかということで通り過ぎることにいたしました。ちゃんと練習せずに大丈夫か？
しかし、その後に「全微分」が登場します。そういえば「全微分」ちゃんとMaximaしてなかったなあ。いつもお世話になっております。東北大様のMaximaの日本語マニュアルページの微分のページが以下に。
https://flex.phys.tohoku.ac.jp/texi/maxima-ja/maxima_18.html
上記から、全微分に関する１か所を引用させていただきます。
del (x)は変数 xの微分を表します。もし独立変数を指定しないなら、 diffは delを含む式を返します。 この場合、戻り値は「全微分」と呼ばれるものです。
わかったような、わからぬような。「ノート」では「変数を指定した」微分では、名詞形＝評価後の式 みたいな見栄えのする形式だったのに、全微分のところでは、敢えて左辺の名詞形を省略しているみたい。そうしている理由を考察せず、微分からの流れで「名詞形＝評価後の式」にしてしまった全微分が以下に。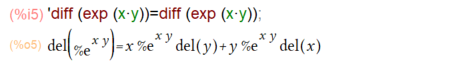
わかったような、わからぬような。大丈夫か。
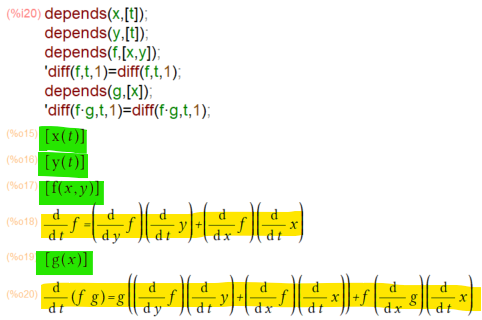
最後は偏微分です。なおMaxima様では、∂記号が使えないので、記号はすべてdになってしまいます。depends()関数で依存関係を宣言しておくと、偏微分がわかりやすいという一件。
以下は演習の行を一部前後入れ替えましたです。
黄緑が依存関係、黄色が微分の結果です。
今回は駆け足で通り過ぎただけ。爾後、演習していかんと。