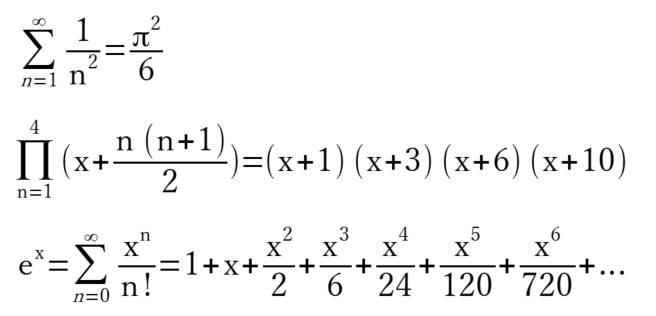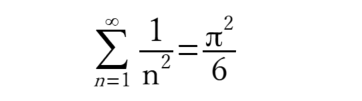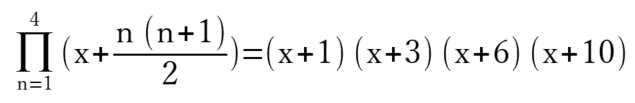前回より、溝口純敏様著「Maxima を使った物理数学基礎演習ノート」（PDFファイル、以下「演習ノート」と略）を読み始めました。全６２４ページ、読めるのか？それどころかこの「演習ノート」４部作の第１作であります。４部作全て読み終えたらMaximaも物理も分かる立派な人になれるとか、なれないとか。ううむ、先は長い。
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- wxMaxima 22.04.0
- Maxima 5.46.0(x86_64-w64-mingw32)
- SBCL 2.2.2 (SBCL = Steel Bank Common Lisp )
※ Maxima を使った物理数学基礎演習ノート は以下のバージョンをダウンロードさせていただきました。
令和4 年3 月 第八回改訂
2.2 級数
今回読ませていただくのは、「2.2 級数」であります。英語にすると Series ってことで良いよね？ Maximaのマニュアルは、いつもお世話になっております東北大様のMaxima日本語マニュアルページの以下あたりが該当するかと思われます。
28. Sums, Products, and Series
まずは級数和から。級数和の例が多数あるなかで演習してみたのは以下一つです。なんでかと言えば、simpsumというオプション変数が「効く」例だったからです。Maximaのsum()関数は知ってましたが、simpsumというオプション変数をtrueにしておくと御利益あらたか。知らんかったです。マニュアルよく読んで使ってないものなあ。simpsumあり、無でこんな感じ。
あれ、これは単純な無限級数和から π が含まれる値がまろび出てくる有名なやつじゃん。
wxMaxima様も精いっぱい頑張って数式を「描いて」くれてますが、Σの記号など、も少し美麗にレンダリングして欲しいっす。別件シリーズでMaximaからのMathMLの出力をLibreoffice Math で受け取って加工するのをやってみました。該当ソフトウエアで使える数式用のマークアップ言語にしてみたものが以下に。
sum from{n=1} to{infinity} frac { 1 } { nitalic n ^ 2 } }= frac {nitalic %pi ^ 2 } { 6 }
その結果の数式表示が以下です。
なんかフォントがイマイチやな。それにイタリックと非イタリックがまざってしまっているし。。。
お次は乗積です。これまたMaxima様が簡素化してくれる例です。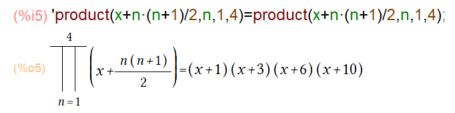
簡単？でも自分じゃゼッテー計算間違えるやつ。やっぱり記号がイマイチでないかい。MathMLの出力をLibreoffice Mathへのルートで作成した数式のマークアップが以下に。
{ prod csup 4 csub { nitalic n = 1 } { ( nitalic x + frac { { nitalic n { ( { nitalic n + 1 } ) } } } { 2 } ) } = { ( { nitalic x + 1 } ) } { ( { nitalic x + 3 } ) } { ( { nitalic x + 6 } ) } { ( { nitalic x + 10 } ) } }
結果の数式が以下に。
悪いけどwxMaxima様の表示よりはこちらの方がやっぱり美麗。
さて、最後は関数 ex を無限級数和とテイラー展開してみるもの。
上記の式をちょいとちょろまかして作成した数式のマークアップが以下に。
nitalic e ^ nitalic x = sum from{n=0} to{infinity} frac { nitalic x ^ nitalic n } { nitalic n nitalic ! } = { 1 + nitalic x + {frac { nitalic x ^ 2 } { 2 }} + {frac { nitalic x ^ 3 } { 6 }} + {frac { nitalic x ^ 4 } { 24 }} + {frac { nitalic x ^ 5 } { 120 }} + {frac { nitalic x ^ 6 } { 720 }} + nitalic ... }
結果はこんな感じ。
遥か昔に習った筈だが、忘れとるの～