別件シリーズのXcosデモで「カルマンフィルタ」に遭遇。デモといいつつちょっと複雑。素人老人は分かった気がしませぬ。そこでWeb上の先達の方々のページを拝見。中でも『logics of Blue』様のページの例が分かりやすかったです。ありがとうございます。元はR言語。今回これを勝手にScilabで書き直してみましたぞ。
※「 ソフトな忘却力」投稿順 Index はこちら
※以下で動かしてみているローカルレベルモデルの「カルマンフィルタ」は、Rと予測と意思決定を御教示されてる『logics of Blue』様の以下ページで例としてあげられているソースを元に、お惚け老人が勝手に Scilab へ移植したものです(後でXcos上に載せる準備として。)
R言語でも、Scilabでもカルマンフィルタを実現するためのライブラリ関数などが準備されていますが、『logics of Blue』様の上記ページでは、ローカルレベルモデル(予測値は前期の値と同じ)を使うことで単純化し、ライブラリを使わないでカルマンフィルタを実装されています。大変勉強になります。ありがとうございます。お惚け老人もRのコードをScilabで書きなおすことで分かったような気がします。ホントか?
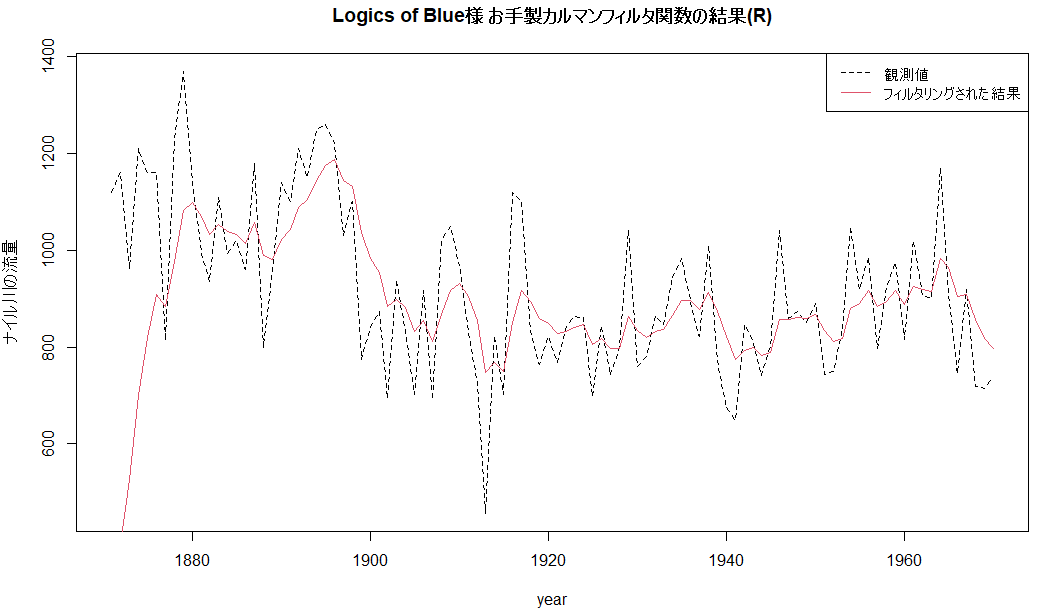
『logics of Blue』様のRのコードの実行結果
上記ページからダウンロードさせていただいた処理例のソースを手元のR環境で実行した結果のグラフが以下に。
LogicsOfBlue_NileKF_R
なお上記でテストデータとして使われているのはエジプトはナイル川の100年間の水量データです。当サイトでも、別件シリーズの以下でちょっと触ってみているもの。
データのお砂場(19) R言語、Nile、ナイル川の水量百年とな?
上記ページからデータ・ソースの解説へのリンクありです。
R言語からScilabへの移植
さて『logics of Blue』様のR言語のソースコードには1行づつ日本語解説もついているので、大変わかりやすいです。これ以上何か必要ということもないのですが、当方、Scilab上のXcos(古くはScicosとも、MATLABのSimulinkのようなソフト)上のフローとしたい、という欲望あり。そのため、勝手ながらR言語からScilabへ移植し、まずは同じ動作をすることを確認させていただくことにしました。
まずはローカルレベルモデルを推定するカルマンフィルタの関数実装部分から。ソースが以下に。
// Original source: Logics of Blue, written in R.
// https://logics-of-blue.com/wp-content/uploads/2017/04/kf-concept-R.txt
// Local Level Model
// Porting from R to Scilab: J. Halfmoon, Feb 9, 2025
// y : Current period observations
// xPre : State of the early period
// pPre : Variance of forecast error for previous state
// sigmaW : Noise variance of the equation of state
// sigmaV : Variance of noise in the observation equation
// xFiltered : Estimated current state
// pFiltered : Corrected state prediction error variance
function [xFiltered, pFiltered] = localLevelModel(y, xPre, pPre, sigmaW, sigmaV)
xForecast = xPre;
pForecast = pPre + sigmaW;
kGain = pForecast / (pForecast + sigmaV);
xFiltered = xForecast + kGain * (y - xForecast);
pFiltered = (1 - kGain) * pForecast;
endfunction
上記の関数を使い、ナイル川の水量データにカルマンフィルタを適用するコードが以下に。
Nile = csvRead('Nile.csv');
N = length(Nile);
x = zeros(N+1, 1);
P = zeros(N+1, 1);
P(1) = 1000;
for i = 1:N
[xFiltered, pFiltered] = localLevelModel(Nile(i), x(i), P(i), 1000, 10000);
x(i + 1) = xFiltered;
P(i + 1) = pFiltered;
end
year = 1871:1970;
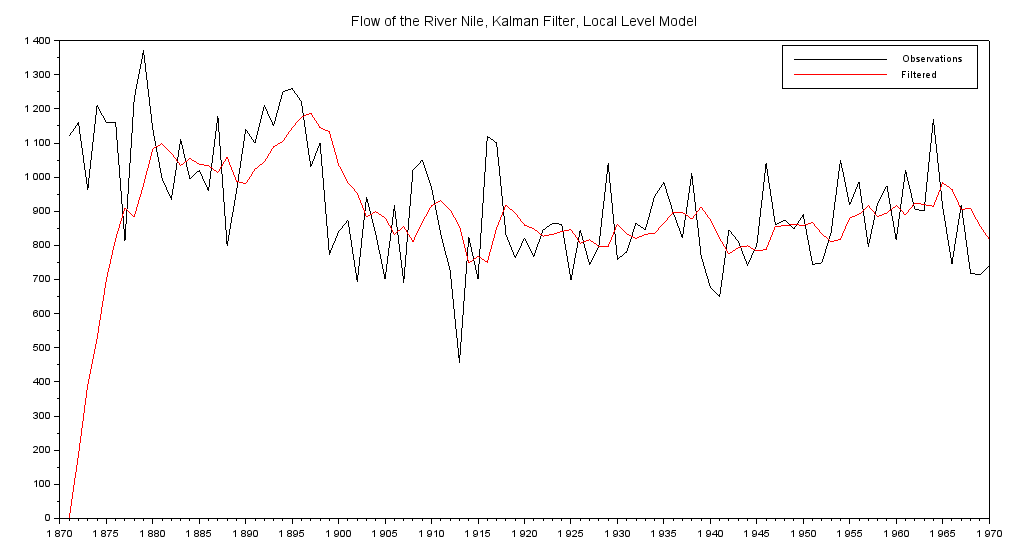
plot(year, Nile(1:100), 'k-', year, x(1:100),'r-');
title('Flow of the River Nile, Kalman Filter, Local Level Model');
legend('Observations', 'Filtered');
移植はできた、と。お惚け老人がカルマンフィルタを理解できているかどうかは別にして。大丈夫か?