溝口純敏様著「Maxima を使った物理数学基礎演習ノート」(PDFファイル、以下「演習ノート」と略)を拝読中。今回読ませていただくのは26ページ目。「3.1.3 微分方程式の数値解:rk 関数」です。rkはRunge-Kuttaです。泣く子も黙るルンゲクッタ法ね。数値解析とか勉強するとイの一番?にやるやつ。
※「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- wxMaxima 22.04.0
- Maxima 5.46.0(x86_64-w64-mingw32)
- SBCL 2.2.2 (SBCL = Steel Bank Common Lisp )
※ Maxima を使った物理数学基礎演習ノート は以下のバージョンをダウンロードさせていただきました。
令和4 年3 月 第八回改訂
Maxima様は数式処理のソフトウエアなので、数式をシンボルのまま解くのがお得意。しかし具体的な数値として扱うことも可能です。常微分方程式を数値で解こうという場合に活躍するのがルンゲクッタ法。それをお手軽に使えるのがrk関数ということみたい。「演習ノート」の今回範囲では、2つほどrk()関数の処理例が挙げられてます。その一つ目の処理例で「目から鱗」なmakelist()関数の使い方があったので、そっちを先に書いておきます。
makelist()の使い方で目から鱗
rk()関数の結果は、「数値を並べたリスト」のリストとして返ってきます。数値を並べただけだとお惚け老人にはサッパリなのでプロットしたいです。勿論Maxima様のplot2d()関数は「ディスクリート」な「数値を並べたリスト」のリストをプロットできるのですが、1点制約あるみたいです。「数値を並べたリスト」の実体は「横軸の値と縦軸の値をならべた2要素のリスト」でないとイケないみたい。
一方、rk()関数は一階常微分方程式一つまたはm個の一階常微分方程式系を解くようにできてます。ぶっちゃけ2階の常微分方程式なら2個の連立方程式系にする必要あり。そしてrk()関数の数値解は、m個の系なら「m+1個の数値をならべたリスト」(最初の1個は独立変数値、残りm個はm個の従属変数値)のリストになるようです。
つまり、プロットするためには「m+1個の数値をならべたリスト」のリストからプロットにご所望の「2個の数値をならべたリスト」のリストを取り出さねばなりませぬ。どしたらよいのよ?
「演習ノート」2つ目の例ではその問題に対して、以下のようなコードで対応してました(一つ目ではグラフ化してません。)
list12:[[sol[1][1],sol[1][2]]]; for J:2 thru Nplot do(list12:append(list12,[[sol[J][1],sol[J][2]]]));
solにrk()関数の返してきた数値解(リストのリスト)が詰まっているので、for文つかって舐めて「2要素のリスト」のリストにアペンドしてました。確かにこの方法でも可能。ただ、恐れ多いことですが、Maxima風にはforとか見たくないっす。気分の問題ね。
そうしたら rk() 関数について解説してくださっている以下のMaximaの日本語マニュアルページに makelist() 関数使ったMaximaらしい書き方が載ってました。
黄色のマーカのところの書き方で、「リスト」のリストの「リスト」内のご所望の要素を取り出して再びリストのリストにできるではありませんか。makelist()という関数は知っていたけれども、こういう使い方は知らんかったです。目から鱗よ。
さてルンゲクッタ法
素人老人が数値解析を語るのもなんなので、いつものようにGoogleの生成AI、Gemini様にルンゲクッタ法についてご説明をお願いしました。こんな感じ。
Maximaのマニュアルページによると、rk()関数に実装されているのは、4次の Runge-Kutta法だそうです。m個の方程式系の場合、m個の要素を持つリストとして方程式を与える必要があるのですが、リストのn番目の要素はn番目の従属変数の導関数と解釈されるようです。リストの要素の順番が大事みたい。
演習
「演習ノート」には2例あがっているのですが、その最初の例はMaximaのマニュアルページに掲載の例と同じ方程式系だと思います。ルンゲクッタ法を適用したところが以下に(最初の部分のみ。)
数値解析なので、この後ダラダラと数値が延々とつづきます。「演習ノート」ではプロットはなく、また、Maximaマニュアルページでもプロット例は掲載されてません。
そこでお惚け老人が自主的にグラフにしてみました。まずは、独立変数 t に対して従属変数 x と y をプロットするもの。
tempX: makelist([p[1],p[2]],p,sol)$ tempY: makelist([p[1],p[3]],p,sol)$ plot2d([[discrete, tempX],[discrete, tempY]],[legend, "x", "y"],[xlabel, "t"],[ylabel, "x,y"]);
さきほど会得したばかりの makelist の使い方を駆使して、[t, x]と [t, y]という2要素のリストに変形してます。各系列は2要素リストのリストだけれども、複数系列を重ねてプロットするのはさらにリストにするだけ。プロット結果が以下に。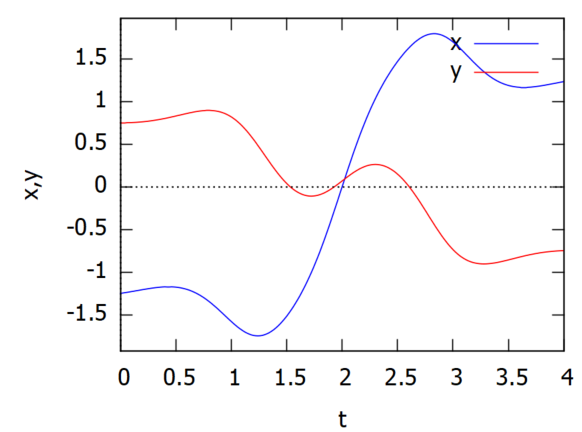
上記は t (横軸)に対する x, y(縦軸) です。
一方、同じtの時の x, y の組を x-y平面にプロットしてみるのも一興ということで以下のようにしてみました。
tempXY: makelist([p[2],p[3]],p,sol)$ plot2d([discrete, tempXY],[xlabel, "x"],[ylabel, "y"]);
何やら不思議な図形よの。なんちゃら空間に引き込まれそうだな。知らんけど。