溝口純敏様著「Maxima を使った物理数学基礎演習ノート」（PDFファイル、以下「演習ノート」と略）を拝読中。今回読ませていただくのは２７ページ。「3.2 一階微分方程式 3.2.1 変数分離形」です。忘却力の老人にも本シリーズの過去回で、なんどとなく練習したような記憶あり。今回はつらつら眺めて通り過ぎるの？
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- wxMaxima 22.04.0
- Maxima 5.46.0(x86_64-w64-mingw32)
- SBCL 2.2.2 (SBCL = Steel Bank Common Lisp )
※ Maxima を使った物理数学基礎演習ノート は以下のバージョンをダウンロードさせていただきました。
令和4 年3 月 第八回改訂
変数分離形
変数分離形は以下デス。
\(\frac {d} {dx} y = f(x) g(y) \)一応上記はLaTeXでレンダリングされている筈なので、LaTeXソースも書き添えます。
\frac {d} {dx} y = f(x) g(y)
例によって、Googleの生成AI、Gemini様に変数分離形について教えてもらいます（変数分離形はみんな大好き？）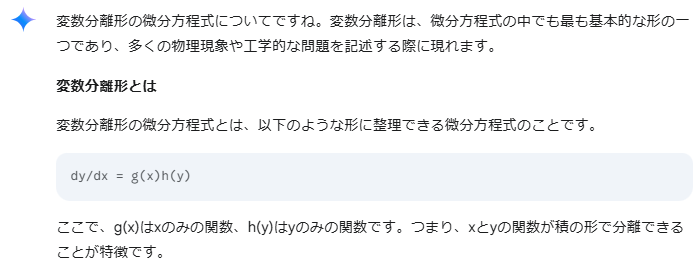
まあ、xのみ、yのみの関数に分離できているので、それぞれ積分してやれば解がでるだろ～ということで上記の後、解法をお教えくださっているGemini様です。
本シリーズの過去回では、「変数分離形」とアカラサマに銘打った回はなかった（手抜きだな）のですが、以下の過去回付近で数度にわたって登場。
忘却の微分方程式(128) 反復練習91、ODE2で微分方程式の一般解、Maxima
そこでのお惚け老人の感想は以下でした。なお、下記の比較相手はdesolve関数です。
『今回のような１階の常微分方程式、変数分離形で一般解を求める例題は ode2 の方が圧倒的に向いている』
「演習ノート」のお教え
一か所、引用させていただきます。
desolve 関数では一部の簡単な問題は解けるが、他はうまく解けなかった。一方、ode2 関数では、全てよい結果が得られた。
ということで「演習ノート」では、ode2使って解いた例が挙げられてます。ま、以前にやって、同様の結論にいたっているし、まあ、今回は「読んだ」ってことでいいか。手抜きだな、大丈夫か？