Scilab/Xcosのデモを動かしながら、Xcosの機能の落穂拾いをしています。今回はみんな大好きフィボナッチ数列です。本サイトでもどこかでフィボナッチしてますが、今回はXcos使って黄金数の逆数へと「漸近」します。その過程で、今まで使ってこなかったXcosの小技を2つほど習得。ううむ、Xcos奥が深いな。
※「ブロックを積みながら」投稿順 index はこちら
※動作確認にはWindows 11の パソコン(64bit)上にインストールしたScilabの以下バージョンを使用しています。
Scilab 2024.0.0
フィボナッチ数列と黄金数
みんな大好きフィボナッチ数列の定義が以下です。
\(\left \{ \begin{aligned} &F_0 = 0 \\ &F_1 = 1 \\ &F_n = F_{n-1} + F_{n-2} ( n \geqq 2 ) \end{aligned} \right. \)
別シリーズの以下の過去回で、Maxima、Mathematicaつかってフィボナッチ数列を計算している回があります。
忘却の微分方程式(26) 数列、総和、級数、MathematicaとMaxima
しかし、今回は黄金数(Golden Number)との関係でフィボナッチ数列が登場します。黄金数は以下ね。
\( \varphi = \frac {1 + \sqrt {5}} {2}\)
そして黄金数とフィボナッチ数列の項の関係が以下に。
\(\displaystyle \lim_{n \to \infty} \frac {F_n} {F_{n-1}} = \varphi\)
このフィボナッチ数列と黄金数の関係について、Google様の生成AI、Gemini 2.0 Flash Thinking (experimental) にお伺いをたてたら以下のようなご回答を得ましたぜ。
今回練習のXcosデモ
さて、今回練習のXcosデモは、デモ選択ウインドウから以下で起動できるものです。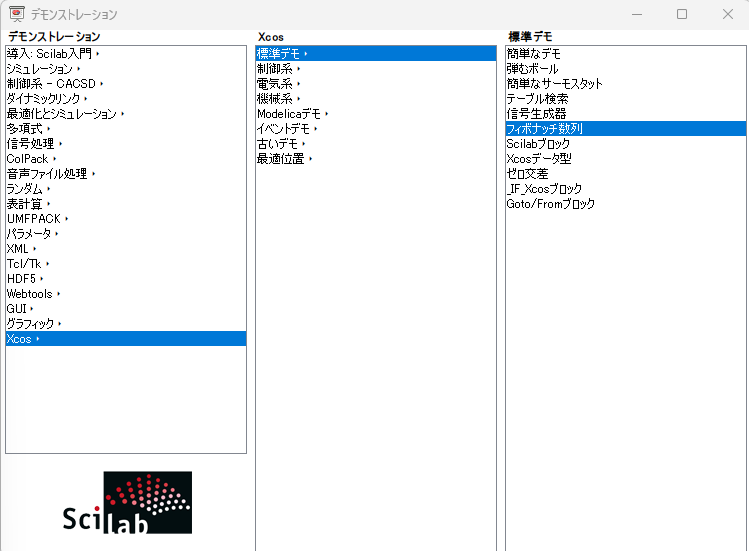
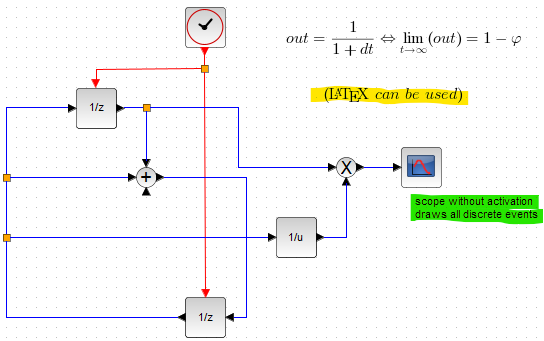
起動直後に、今回のTIPS2つが書かれてました。
-
- Xcosでも、LaTeX表記有効(黄色のマーカ)
- イベントポートによるアクティベーションなしのスコープでディスクリートなイベントをプロットできる(緑色のマーカ)
知らんかったよ。
上記のフローを見てもアカラサマにフィボナッチ数列の漸化式は書かれてませんが、「1/z」は遅延オペレータである、と思って上の1/zが保持しているのがnの項、下の1/zが保持しているのがn+1の項だと思えば、その間に+があってフィボナッチ数を計算していることが分かります。
また、1/uと掛け算のブロックをみると、Fn÷Fn+1を計算していることになるので掛け算の結果が、黄金数の逆数になっていることが分かります。フローの計算結果の極限は、1/φ なのに 殊更に out 以下の極限をわざわざコメントに書いてある意図は、数学素人老人には分かりかねます。なんだかな~。
なお、別シリーズの以下の過去回にて、MaximaからのLaTeX出力、そしてWordPress上でのLaTeX表示について調べてます。
ソフトな忘却力(68) MaximaのLaTeX形式出力をタイプセットして~
ソフトな忘却力(72) WordPress上のLaTeX数式表示、MathJaxでお楽
実際にXcosのコメントでLaTeX表記使っているところが以下に。
上記のウインドウは右クリックから書式>編集で開きます。
初期値の設定と黄金数(ゴールデン・ナンバー)の逆数への漸近
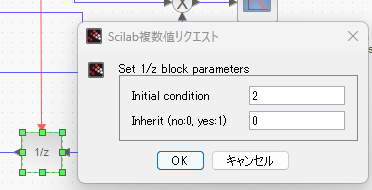
2つの遅延演算子「1/z」には初期値が与えられてます。上が、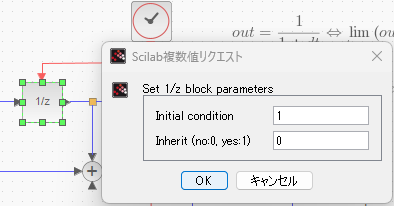
ちょっと端折っている気がしないでもないが、フィボナッチ数列の出だし付近の2項であります。
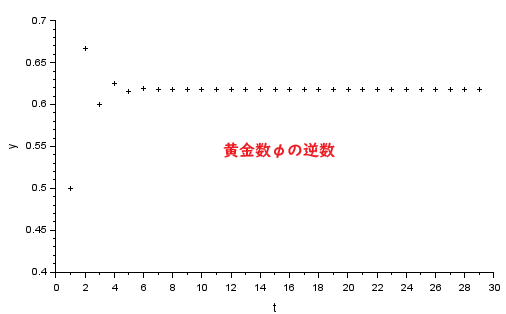
なお、黄金数の逆数を計算してみると
約0.6180339887498948
です。期待どおり?