
信号処理素人老人が、Scilabの「信号処理のデモ」調査中。前回は素人老人にも理解できるFIRフィルタでしたが、今回はWiener推定とな。そしてその裏に「カルマン様」の影がチラチラと見えてます。おっとヤバイよ。デモといってポロリンとグラフ一枚くださっても何が何やら?またまたGemini様におすがりするしかない?
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※Windows11上の Scilab2024.0.0を使用させていただいております。(Scilabについては御本家 Scilab 様へ)
今回動かしてみるデモ
以下のScilabデモ選択ウインドウから「ウイナーフィルタ」を選択すると実行できるのが今回のデモです。
今回も信号処理素人老人にはサッパリっす。例によって、Google様の
Gemini 2.0 Flash Thinking(experimental)
「誤差の二乗を最小にする」というのはいつものアレですが、その先がムツカシーです。その上、老人が勝手に赤枠つけて黄色のマーカ引きましたが、今回の処理には「未来の信号」からの逆算過程も含まれているみたい。それだけに元の信号の推定の精度は高いけれども、当然リアルタイムに計算できる訳ではない。後付け?
Gemini様はWienerフィルタの利点、欠点についてもお教えくだすっているのでその部分も引用。
デモ実行
「見る前に飛べ」(偉大な作家様のお言葉デス)とばかりに実行したデモの結果に勝手に信号処理素人老人のコメントを付け加えたグラフが以下です。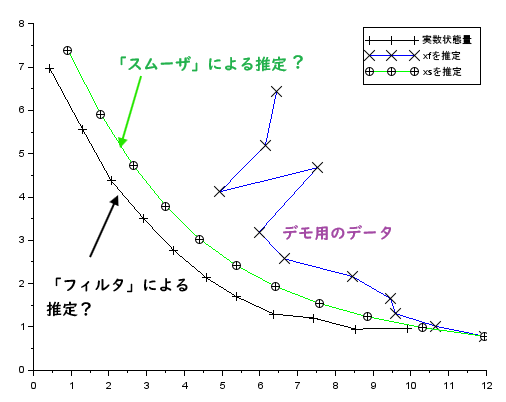
「実数状態量」というのは、デモ用に作られたデータということで良いのかな。でも、トートツにxfとかxsとか言われてもなんのこっちゃ。まあ、ソースコードとHelpファイルをGemini様のお導きで読み解いたところ、以下のように「推定」いたしました。
-
- xf ⇒フィルタリング(カルマン・フィルタ)された状態推定値
- xs ⇒スムージング(カルマン・スムーザ)された状態推定値
つまり、デモ用の「ノイズてんこ盛りのがたがたなデータ」をフィルタに通すとそれなりの推定ができるけれども、さらに、「未来の値から遡る」ようなスムーザを適用するともっとだと。分かったような分からぬような。
デモのソース(冒頭部分)が以下に。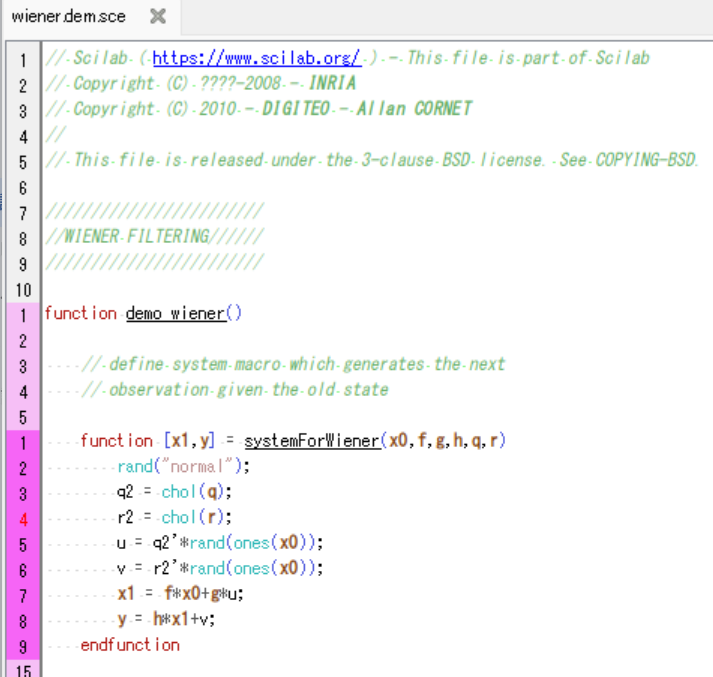
なお、上記のソースファイルのお名前は以下です。
wiener.dem.sce
上のソースの流れをお惚け老人が「推定」すると以下のような感じでないかと。
-
- デモのターゲットとなるシステム関数(状態空間モデル)を定義
- 上記関数に基づき解析対象となる人為的なサンプルデータ列ytを生成⇒これには乱数使ったノイズがのっている
- wiener関数によりWiener推定
- 結果をプロット
上記はデモ用とて人為的なデータ生成のステップです。多分、実データに適用する場合は、以下のようになるんではないかと。知らんけど。
-
- 解析対象の実データ列yがある
- 実データについて想定されるモデル(システム行列)と、ノイズ(共分散行列)が考案されている
- wiener関数によりWiener推定を行う
- 結果をプロット
さてこの中心になっているのが wiener関数です。この関数は、Helpファイルによると、
フォワード-バックワードカルマンフィルタ定式化(Forward-Backward Kalman Filter Formulation)
を行う関数らしいです。あらえっサッサ。またもやGoogleの生成AI、Gemini様にお教えいただきます。
ということらしいっす。そして、カルマンスムーサーについても以下のように述べられてます。
Gemini様のいう通りっと。お惚け老人は暗の中で手探りで惑っているというのに。
