溝口純敏様著「Maxima を使った物理数学基礎演習ノート」（以下「演習ノート」と略）を拝読中。今回は３２ページ「3.2 一階微分方程式 3.2.7 Clairaut の微分方程式」です。最近Maximaの例題をGoogleの生成AIに解いてもらってますが、今回から使用AI変更？よりフツーなやつなんだけど解けるの？
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- wxMaxima 22.04.0
- Maxima 5.46.0(x86_64-w64-mingw32)
- SBCL 2.2.2 (SBCL = Steel Bank Common Lisp )
※ Maxima を使った物理数学基礎演習ノート は以下のバージョンをダウンロードさせていただきました。
令和4 年3 月 第八回改訂
※ 方程式の解を求めるのに Googleの生成AI、Gemini 2.0 Flashを使わせていただきました。
使用させていたたくAIの変更？それとも同じもの？
これはGoogle様の変更を反映しただけのことですが、前回までは、
Gemini 2.0 Flash Thinking (experimental)
を使わせていただいておりました。experimentalデス。ところが今回Geminiのページを開いてみると上記の選択肢は消滅。アイキャッチ画像に示したとおりで、2.0からはexperimentalという注意書きが消え、2.5がexperimentalとなっとりました。根が小心者で保守的なので、今回は experimanetalでなくなった（そしてThinkingというタイトルも消えた）Gemini 2.0 Flashにスイッチというか継続利用というかです。
Clairaut の微分方程式
数学素人老人が、クレローの方程式について何もいいますまい。前回同様 y’のべき乗など含む「高次」の方程式っす。Gemini様にお伺いをたててみると以下のごとし。
黄のマーカはこちらで塗ったものっす。
上記の後、実際に例を引いて解き方が解説されておりましたが、以下で「演習ノート」の例題についてGemini様に解いてもらうので省略しました。
「演習ノート」の例題
まず演習ノートの例題をそのまま、ode2関数に渡してみると、y’の二乗の項など含まれるのでダメダメです。これは想定内。
解き方は「演習ノート」にしっかり記されているので、以下のようにdy/dx=pとおいた後は、丸写しに近いデス。
P1:diff(y,x,1)=p;
p1で置換して、微分したものをp=の形で書き直しているみたい。
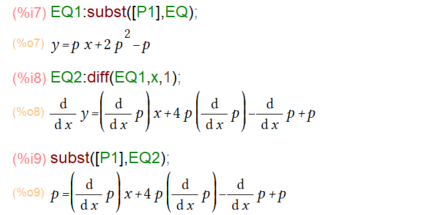その後、一般解（青色マーカ部）、そして特殊解（赤色マーカ部）を求めていきます。
それなりに手数かかるべし、と。
Gemini様にお願いしてみると
「日常的タスク」な選択肢のGemini様ですが、クレローの微分方程式など一撃という感じデス。Gemini様には日常なのか。。。
上記の後、特異解を求めるところ、結構ステップを踏んで、懇切丁寧にお教えくだすっているのですが、端折りました。最後の結果が以下に。
やっぱり数学素人老人など要らんな、Gemini様にお願いするだけじゃん。