手習ひデジタル信号処理(183) Scilab、{Scilabデモ}、ARMAその１

信号処理素人老人がScilabの「信号処理のデモ」物色中デス。今回はARMAモデルです。あらまー、言うと思った。時系列データの解析と予想に使われる「アレ」です。Scilabでは、CACSDの部に、ARMA関係の関数どもが多数含まれてます。今回は人為的なサンプルデータを「でっち上げて」そこからパラメータを同定してみると。

※「手習ひデジタル信号処理」投稿順 Indexはこちら

※Windows11上の    Scilab2024.0.0を使用させていただいております。（Scilabについては御本家 Scilab 様へ）

※自己回帰モデリング（ARMAは「定常時系列モデル」「自己回帰移動平均モデル」である）に関する忘却力の老人の備忘録はこちら

ARMA

ARMAあればARIMAなどもあり。ScilabではCACSD（Computer Aided Control System design）のところに「ARMA関係」の関数どもが多数含まれてます。いつものように、ARMAについて、Googleの生成AI、Gemini 2.0 Flash様に解説していただきましたぞ。

上記、Gemini様のご説明の中に赤枠で囲んだ部分、覚えておいてくだされや。忘却力の年寄りには記憶できんけど。

さて、Gemini様のご説明は続きます。

ここで再び、φだのθだののパラメータ登場、そしてそれらの次数がpとqね。

注意点が以下に。

例によって分かったような、分からぬような。。。

今回のデモ

今回試行してみるデモは、以下のデモ選択ウインドウから実行できる「ARMAシミュレーションおよび同定」というものです。

実行すると表示されるグラフが以下に。

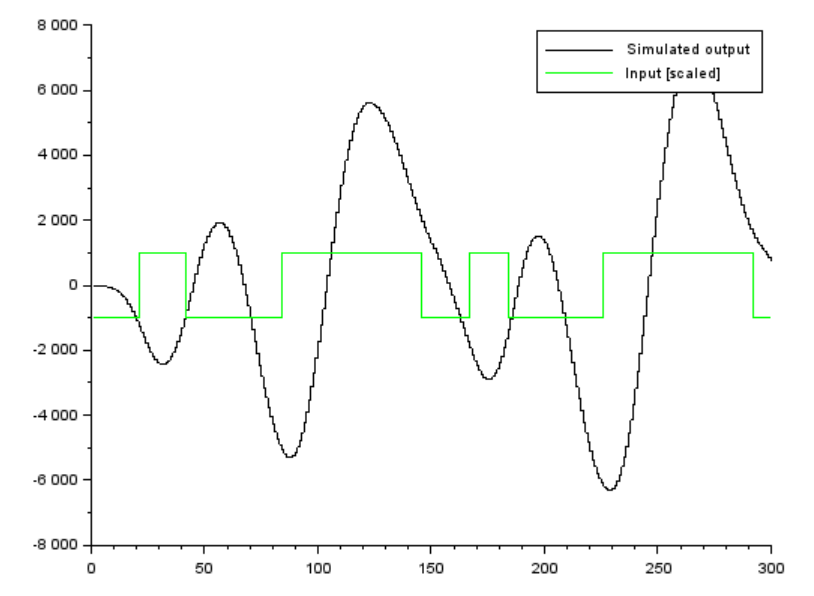
ただし、このグラフは「結果」ではありませぬ。ARMAモデルで同定する人為的な時系列入力データです。緑色は疑似ノイズ系列、黒色がARMAモデルで生成（シミュレーション）される時系列データです。

上の黒のデータを「同定」のための関数に突っ込むとあ～ら不思議、ARMAモデルのパラメータ（上記のgemini様のご説明にあるφ、θに相当する値）が推定されるようです。

例によってデモコードを読むとこんなシナリオみたい。

1. 1. armac（armaxデータ構造体）に人為的なデータを与えて作成する。なおScilabでは、p、 q、φ、θ、cという前述の変数名に変えて、A、B、D（線形システムのアレ）、ny、nu、sigという変数名になるのでイコールではありませぬ。例えばAとBからφが求まるみたいな関係性？知らんけど。
   2. 上記で定義したデータ構造体に、prbs_a関数で生成した「疑似乱数系列」を加えて、narsimul関数でシミュレーション。するとARMAモデルで紡がれた時系列データ（人為的なサンプルデータ）が得られる。
   3. 上記時系列データをプロットしたものが前述のグラフ
   4. 上記時系列データを armax関数と armax1関数に「突っ込む」とARMAモデルのパラメータどもの推定値が得られる（モデルのパラメータが分かれば、「予想」も出来るハズってこってすかい？ここではやらんけど。）

なお、上記の推定値（およびその元になった設定値）はScilabのコンソール画面にテキスト表示されます。まずは設定値から。こんな感じ。

 "ARMAX過程のシミュレーション:"
A(z^-1)y=B(z^-1)u + D(z^-1) e(t)
"A(x) ="
1 -2.851x +2.717x^2 -0.865x^3
"B(x) ="
x +x^2 +x^3
"D(x)"
1 +0.7x +0.2x^2
e(t)=Sig*w(t); w(t) 1-dim white noise
Sig= | 1 |

上記のモデルに対して、緑の乱数系列突っ込むと黒の時系列データが出てくるのだと思います。

一方、同定結果とarmax関数で推定されたパラメータが以下に。

"ARX同定 (最小二乗):"
armax: 推定器の標準偏差 a:
0.00000 0.00669 0.01319 0.00655
armax: 推定器の標準偏差 b:
0.00000 0.20449 0.28427 0.22867

A(z^-1)y=B(z^-1)u + D(z^-1) e(t)
"A(x) ="
1 -2.8642788x +2.7430047x^2 -0.8778367x^3
"B(x) ="
1.2923839x +0.9496763x^2 +0.6193817x^3
"D(x)"
1
e(t)=Sig*w(t); w(t) 1-dim white noise
Sig= | 1.2919365 |

上記みるとDはぜんぜんだけれど、A、B、Sigとかはそれなり？いいのかそういうことで。

一方、お次のarmax1の結果が以下に。

 A(z^-1)y=B(z^-1)u + D(z^-1) e(t)
"A(x) ="
1 -2.8630931x +2.7406521x^2 -0.8766667x^3
"B(x) ="
1.1815018x +0.9675865x^2 +0.6678505x^3
"D(x)"
1 +0.2526456x +0.0423768x^2
e(t)=Sig*w(t); w(t) 1-dim white noise
Sig= | 1.1367633 |

なんか、後のやつの方がよさげに見えるが、お惚け老人は２つの関数の算法の違いを理解していないのでサッパリっす。ま、推定できてるみたいなので、まあ、いいか？　いいのかそういうことで。

手習ひデジタル信号処理(182) Scilab、{Scilabデモ}、2次元畳み込み　へ戻る