信号処理素人老人がScilabの「信号処理のデモ」物色中デス。今回はARMAモデルの3回目です。前回はクロネッカー積が登場し目を回しました。 今回は「エントロピー・スペクトル」です。止めてケレ。半世紀前くらいにエントロピーで落ちこぼれた記憶。エントロピーのスペクトルって何?困ったときのGemini様だのみ。
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※Windows11上の Scilab2024.0.0を使用させていただいております。(Scilabについては御本家 Scilab 様へ)
※自己回帰モデリング(ARMAは「定常時系列モデル」「自己回帰移動平均モデル」である)に関する忘却力の老人の備忘録はこちら
※素人老人の分からぬことは、Googleの生成AI、Gemini 2.5 flash様 に解説いただいております。いいのか、そういうことで。
ARMA、スペクトルパワー推定
今回練習させていただくデモは、以下のデモ選択ウインドウから選択できるものです。
スペクトルなどと言われると、ついFFTにお願いしたくなりますが、どうもそういうものじゃありません。
スペクトル推定の最大エントロピを求める
らしいです。ヤバイよ。エントロピーだよ。何度聞いても約半世紀前に落ちこぼれた記憶が蘇るお言葉です。これぞ他力本願、Googleの生成AI、Gemini様におすがりしてしまいました。なお、気がついたらGemini様は2.0から2.5にバージョンアップされてました。
ううむ、いつものことですが、分かったような、分からぬような。
上記の解説の後にエントロピースペクトルの応用についてのご説明がありました。こんな感じ。
今回は、「2」のカテゴリの時系列データ解析であります。そこには「最大エントロピー法」が掲げられてますが、デモコードを調べてみると別なアルゴリズムでした。
デモのソース
デモのソースコードは以下のファイルに格納されています。
arma3.dem.sce
素人老人が、上記ソースを拝見するに、以下のようなステップでした。
-
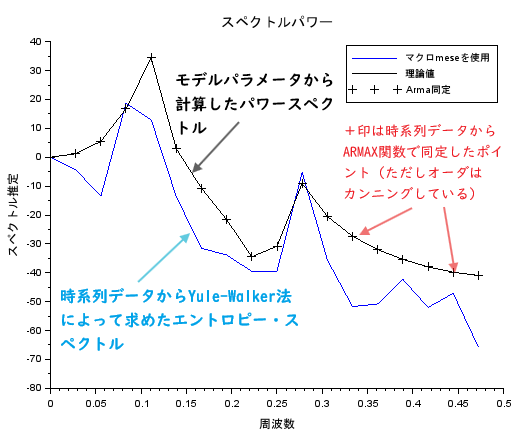
- 既知のモデルパラメータから時系列データをシミュレーションする
- 上記のシミュレーション結果(時系列データ)からmese関数(マクロ)をつかって「エントロピー・スペクトル」を推定
- 比較のため、シミュレーションにつかったパラメータから「エントロピー・スペクトル」の理論値を求める
- 時系列データから、ARMAモデルのパラメータをarmax関数使って同定する。ただしモデルのオーダーは「既知のモデルパラメータ」を知っている前提(ズルしている。)
なお、2番のmese関数(マクロ)ですが、内部でlev関数を呼び出してました。これは、「LevinsonのアルゴリズムによりYule-Walker方程式を解いてAR係数を求める」関数みたいっす。Yule-Walker法について、再び Gemini様におすがりしました。
これまた、分かったような、分からぬような。
また、3の「エントロピー・スペクトル」の理論値については Gemini様は以下のようにお教えくだすってます。
なお、『最大エントロピー法で推定されるスペクトルは、AR モデルのパワースペクトルと等価』らしいです。
デモの結果
ようやくグラフの意味が分かったような、分からぬような。トホホ。。。