
「サイエンティフィックPythonのための」IDE、Spyder上にてScientific Python Lecturesの実習中。前回はODEの初期値問題。今回はFFT(高速フーリエ変換)を流したいデス。 「流す」には理由があり。この後「本命」信号処理のモジュールが登場するためです。そっちでミッチリ練習する予定。
※「 ソフトな忘却力」投稿順 Index はこちら
※Scientific Python Lectures様のコースは例題だけでなく、エクササイズなども充実、それを全部順番に解いていったら必ずや立派な人になれるだろ~と思います。でも老い先短い年寄には量が多過ぎて多分死ぬまでに終わりません。適当な練習でお茶を濁してます。今回の「お勉強」は「5.8 Fast Fourier transforms: scipy.fft」です。
FFT
レクチャでは1次元の例を挙げたあと、2次元画像に対してFFTを適用するExcersizeなどやってます。その辺、別シリーズで何度なくやったな~などと思いながら、今回は1次元でお馴染みのFFTのグラフを一つ描いてお茶を濁したいと思います。
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Tue Jul 1 2025
@author: jhalfmoon
FFT sample
"""
import numpy as np
import matplotlib.pyplot as plt
import scipy as sp
def main():
N = 4410 # 44.1kHz * 1/10
T = 1.0 / 44410.0 # sampling interval
x = np.linspace(0.0, N*T, N, endpoint=False)
y440 = np.sin(440.0 * 2.0 * np.pi * x)
y4186 = np.sin(4186.0 * 2.0 * np.pi * x)
y = y440 + 0.1 * y4186
yf = sp.fft.fft(y)
xf = sp.fft.fftfreq(N, T)[:N//2]
plt.subplot(2,1,1)
plt.plot(x, y)
plt.title("Signal: 440Hz + 4186Hz")
plt.subplot(2,1,2)
plt.semilogy(xf[1:N//2], 2.0/N * np.abs(yf[1:N//2]), '-b')
plt.title("FFT sample plot: 440Hz + 4186Hz")
plt.grid()
plt.tight_layout()
plt.show()
if __name__ == '__main__':
main()
伝統のサンプリング周波数44.1kHz、にて10分の1秒分の音声波形を作り、その波形の実時間波形を観察した後、FFTにかけた結果を眺めてます。波形は440Hz(「ラ」の音、どこの?)と4186Hzの音声を重ね合わせたものです。ただし、4186Hzの方は振幅を10分の1にしてあるので、実時間波形を見れば、ほぼほぼ440Hzの波形に見えるハズ。
スクリプトの実行結果
実行結果の波形が以下に。上が実時間波形、下がFFTの結果です。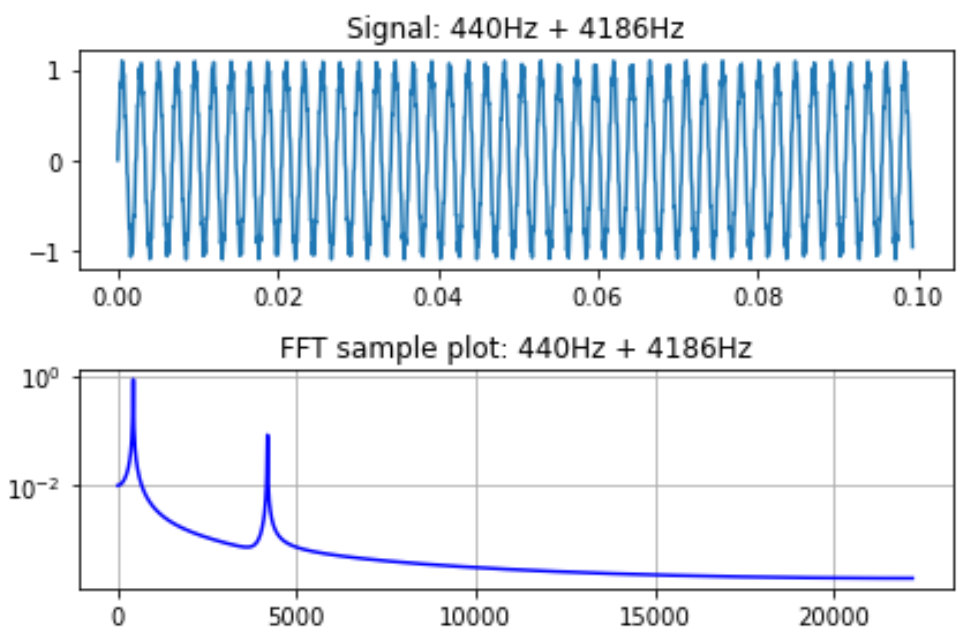
上の実時間波形はほぼほぼ440Hz単独に見えますが、微妙に波形がガタついている部分あり、多分これがわずかにのぞく4186Hzの名残なのだと思います。
下のFFT波形をみれば、周波数は明らか。440Hzと4186Hzと思われるあたりにピコンとピークが描かれてます。
まあ、次回以降、信号処理のところが楽しみじゃて。