MASSパッケージのサンプルデータセットを巡回中。大文字優先のABC順。前回は自動車保険のデータでした。順当にABC順では今回はMelanomaなのですがパスして、OMEです。幼児の滲出性中耳炎の検査データに進みます。乳幼児の場合、OMEが原因で言葉の獲得が遅れたりもするみたい。今回は処理例充実過ぎ、ムツカシー。
※「データのお砂場」投稿順Indexはこちら
Melanoma飛ばしの理由
melanoma、悪性黒色腫は怖ろしい御病気です。忘却力の老人が過去回を振り返る(検索しただけ)と、既に2回も同名のサンプルデータセットに遭遇してます。今回、MASSパッケージで遭遇したものは、以下の過去回で遭遇したものと同じデータセットではないかと思われます。
データのお砂場(123) R言語、melanoma、悪性黒色腫の生存データ、{boot}
第166回でもmelanomaに関するデータセットを扱っているのですが、こちらは異なるデータセットです。
OME、滲出性中耳炎
素人老人が、「中耳と耳管の断面図と症状の説明」が手短にならんでいるページを探したところ、以下を見つけました。ありがとうございます。
「社会福祉法人 恩賜財団済生会」様
どうも中耳に液体が詰まって抜けなくなり、耳がよく聞こえなくなる御病気みたい。今回のデータは乳幼児の検査データらしいです。とくに症状を伝えることができない乳幼児にこれが起こるといろいろマズイからみたいです。サンプルデータセットの解説ページが以下に。
Tests of Auditory Perception in Children with OME
サンプルデータにはAgeという列があり、30とか60とかデカイ数字が書いてありますが、月齢です。30か月(2歳半)と60か月(5歳)が中心みたいですが、7か月などという小さなお子様のデータも混じっています。どういう試験方法なのか詳細は不明ですが、広帯域のノイズの中から信号となる音声を判別する試験らしいです。かいつまむと
-
- 数十人のOMEのお子様にノイズ混じりの信号をきかせる
- 75%の正答率を得るのに必要な信号音量(デシベル)を閾値とする
- ノイズの与え方にコヒーレントとインコヒーレントの2つの方法がある
ということみたいです。
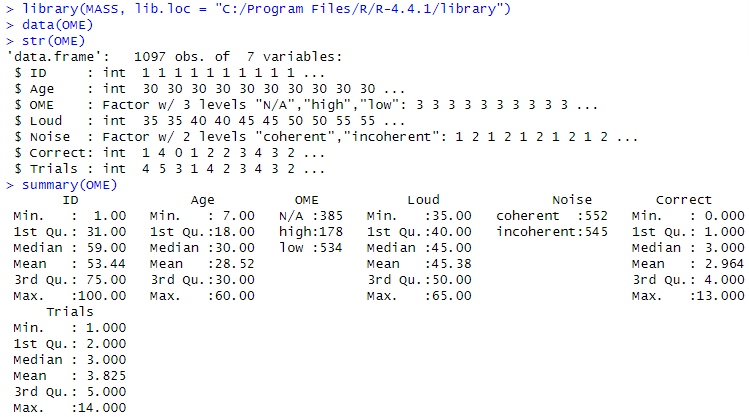
先ずは生データ
これだけ眺めてみてもなんだかな~
今回は処理例充実
MASSパッケージについては、処理例などが見当たらないものが多いです。しかしこのOMEデータについては別です。ガッツリ充実した(しすぎた)処理例が付属しています。最初の部分を実行してみたところが以下に。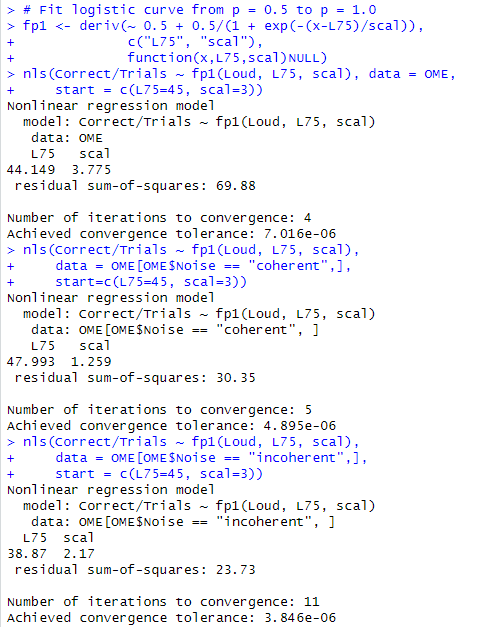
おお、もっと分からなくなったぞ。だいたい deriv関数も nls関数も使ったことがないです。そして上記の3~4倍の分量の処理例がこれにつづいてます。みなムズカシそー。
千里の道も一歩より、とて上記の最初の部分、deriv関数から見ていきます。deriv関数は「記号微分」を行ってくれる関数みたいです。シンボルで式を与えるとその「微分」が計算できる関数を返してくれるものみたい。Maxima様でよくやる数式処理と似たようなことを(でも結果は数字で返る)R言語でもできるのね。ホントか?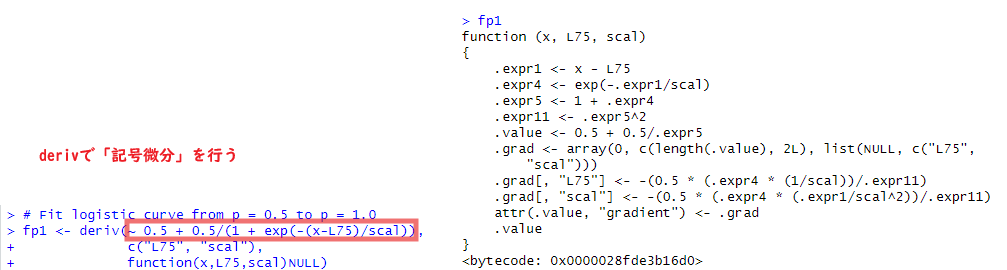
上記では赤枠の式を記号微分した結果の関数を右側に表示してあります。引数あたえりゃ勾配が返るのか?
さて、上記で定義した勾配関数を使ってnls関数、非線形最小二乗法(Nonlinear Least Squares)を使って、曲線にフィットさせ、そのパラメータを推定しようというのです。ちょうど最近、以下の別件シリーズで
ソフトな忘却力(95) SciPy.optimize でカーブフィッティングのお勉強
カーブフィッティングやってます。SciPyでやってることはR言語でも出来るのね。まあ、いろいろ出来ることは知っていたけども。流石ね。
処理のところを順番に見ていくと
-
- 一種のロジスティクス回帰モデル(パラメータはL75、scalという数値らしい。上記の赤枠式にあり)とを想定しているみたい
- 最初にOMEデータ全体に対してモデル適用
- 次にcoherentデータに対してモデル適用
- 最後にincoherentデータに対してモデル適用
上から下へ行くにつれて、残差が小さくなっていくみたいなので、フィットする塩梅は良くなっているってことみたい。
とりあえず、ここまでのトコロをグラフに
上記のカーブフィッティングの結果のところまでを無理やりグラフにしてみました。グラフ上にカーブをプロットするために以下を定義しておきます。
L <- seq(35, 65, 1)
LogModel <- function(x, L75, scal) {
res <- 0.5 + 0.5/(1 + exp(-(x-L75)/scal))
return(res)
}
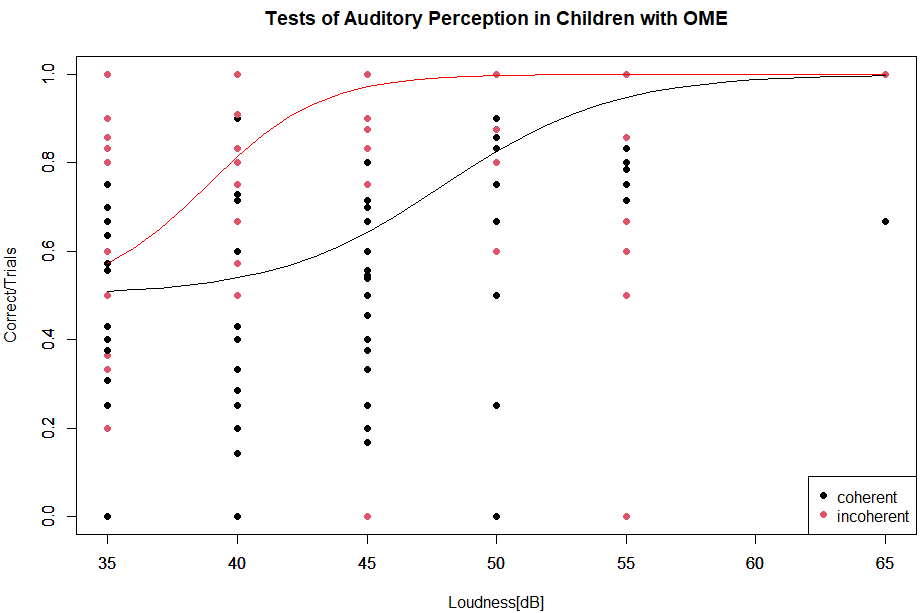
横軸にLoud(音量、dB単位)、縦軸に成功率?(CorrectをTraialsで割ったもの)をとって、OMEサンプルデータをプロット(コヒーレントが黒、インコヒーレントが赤)した上に上記のカーブフィッティングの結果の曲線を重ねて描いてみます。
plot(OME$Correct/OME$Trials ~ OME$Loud, xlab="Loudness[dB]", ylab="Correct/Trials", col=OME$Noise, pch=16, ylim=c(0, 1))
par(new=T)
plot(L, LogModel(L, 38.87, 2.17), type="l", col="red", ann=F, ylim=c(0, 1))
par(new=T)
plot(L, LogModel(L, 47.993, 3.259), type="l", col="black", ann=F, ylim=c(0, 1))
title(main="Tests of Auditory Perception in Children with OME")
legend("bottomright", legend = levels(OME$Noise), col = OME$Noise, pch = 16)
まあ、描くには描けたが、分かったような分からぬような。いつもだな。
このまだ3~4倍も処理例が続くのよ。実行はしてみたものの、理解が追い付きませぬ。