
溝口純敏様著「Maxima を使った物理数学基礎演習ノート」(以下「演習ノート」と略)を拝読中。今回は65ページ「3.4.4 Legendre の微分方程式」です。アドリアン=マリ・ルジャンドル様の御名前を冠する方程式のご出座。Gemini様の御教え読んだ後、演習ノートのルジャンドル多項式のMaxima様グラフを描画。
※「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- wxMaxima 22.04.0
- Maxima 5.46.0(x86_64-w64-mingw32)
- SBCL 2.2.2 (SBCL = Steel Bank Common Lisp )
※Maxima を使った物理数学基礎演習ノート は以下のバージョンをダウンロードさせていただきました。
令和4 年3 月 第八回改訂
Legendre の微分方程式とその一般解、そしてLegendre の多項式について
「演習ノート」は各ステップ着実に計算して、一歩一歩進んでいくのです。しかし忘却力の老人は、読んでいる(Maxima様に計算お願いしている)うちに前のステップを忘れてしまうくらい長大。今回も先にGoogleの生成AI、Gemini 2.5 Flash様による概要を読んでしまいました。こんな感じ。
上記でGemini様がνと綴られているシンボルは、演習ノートではNとなってます。また各項の符号の正負が引っくり返っているよし。
Gemini様には「ルジャンドル微分方程式の一般解を教えて」とお願いしているので、途中経過なく、一挙に一般解をお教えくだすってます。そしてここから「ルジャンドルの多項式」への道筋も提示していただいとります。
さてその後は、ルジャンドルの多項式についてのご説明が続きます。こんな感じ。
分かったような、分からぬような。
ルジャンドルの多項式(nが整数のとき)のグラフ
素人老人の勝手な理解では「演習ノート」では、下のような流れで説明がされています。
-
- Gaussの方程式に変形
- 解を超幾何関数Fをつかって求める
- ただしx=1では発散する
- x=0を中心に展開する級数解を求める(下の2つにわけて計算)
-
-
- 係数a(n)のnが偶数のとき
- 係数a(n)のnが奇数のとき
-
肝心な上記の部分は、演習ノートに書いてある通りということで(真面目にやれよ。)ここはMaxima様にお願いして、最後、「Legendre の多項式、N=0~7のグラフを描くところ」を再現してみました。グラフはよい感じなのよ。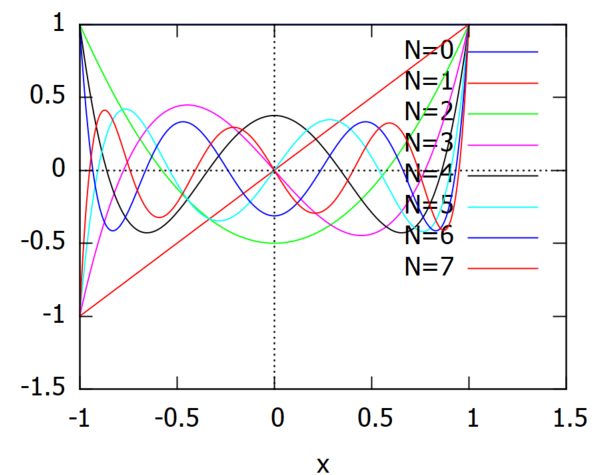
Legendre の多項式なんだよなあ、知らんけど。

