
溝口純敏様著「Maxima を使った物理数学基礎演習ノート」(以下「演習ノート」と略)を拝読中。今回からついに76ページ「第4章 ベクトルとテンソル」に突入。まずはベクトルから、ということで気づきました。Maximaにおけるベクトルの表記法に2流派があり。「演習ノート」の御家流はどうも過去回で使っていた流派とは違う?
※「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- wxMaxima 22.04.0
- Maxima 5.46.0(x86_64-w64-mingw32)
- SBCL 2.2.2 (SBCL = Steel Bank Common Lisp )
※Maxima を使った物理数学基礎演習ノート は以下のバージョンをダウンロードさせていただきました。
令和4 年3 月 第八回改訂
過去回でのベクトル表記の御家流
ベクトル表記に2流派あり、といえども、どちらの流派をとっても必要なベクトルの計算は出来るみたいです。ただ、コマケーところで若干の違いが出てくるので注意。
-
- 第1の流派、リスト([と]の間に成分をカンマで区切って並べたもの)をそのままベクトルとみなす。どうしても列ベクトル表現したい場合にはtransposeする。
- 第2の流派、Matrixの中で 1xN 配列を行ベクトル、Nx1配列を列ベクトルとして使用
過去回では第1の流派に基づいて処理しています。まず以下の過去回では、MathematicaとMaximaにおける「ベクトル」表記をちょこっと比べてます。
忘却の微分方程式(30) ベクトル解析その1、MathematicaとMaxima
泣く子も黙るMathematicaは、数式処理ソフトの金字塔?フツーは有料なソフトウエアですが、Raspberry Pi OSでの「特例」的な扱いでフリーで使わせていただいたものです。Mathematicaでのリストは中かっこ{}表記ですが、第1の流派同様の方法でベクトル計算できます。Maximaよりかベクトル専用の演算子や関数など充実している雰囲気あり。
また、Maximaにおける第1の流派の例は過去回に多数あり、その一部が以下に。
忘却の微分方程式(37) 反復練習1、ベクトルに垂直な単位ベクトルを求める、Maxima
忘却の微分方程式(50) 反復練習14、列ベクトルの内積となす角Θ、Maxima
忘却の微分方程式(169) Maxima、{vect}、ベクトル解析パッケージ再び
とくにMaximaをインストールすると漏れなく付属してくる
-
- plotdfパッケージ
- vectパッケージ
でも、第1の流派の書き方で問題なかったデス。
しかし演習ノートで「推して」いるのは、Matrixをつかう流派デス。今まで使ったことが無いので、ここは何でもお見通しのGoogleの生成AI、Gemini 2.5 Flash様に教えてもらいました。こんな感じ。
そうなのね~。次回以降は、演習ノートの御家流でMatrix使った方法を学んでいきたいと思います。
2つの比較
2つの流派で、行ベクトル、列ベクトルを生成するところが以下に。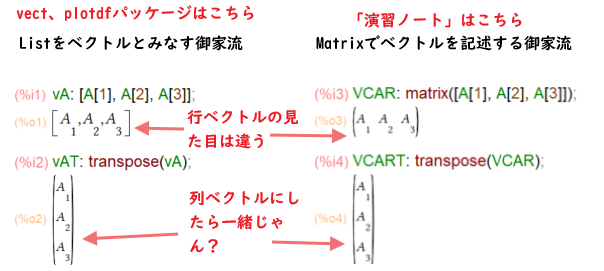
行ベクトルの見た目(実態も)は違うケド、列ベクトルにしたら一緒に見えますな。
第1の流派のスタイルだと、行ベクトルは行列ではないので行列サイズを知ろうとすると上記のようにエラーになります。一方、第1の流派のスタイルでも転置して求める列ベクトルは行列サイズあり。勿論、第2の流派は行でも列でもサイズは求まると。
次回以降、練習しながら、コマケー話があったら適宜かきとめていこうと思います。
