溝口純敏様著「Maxima を使った物理数学基礎演習ノート」（以下「演習ノート」と略）を拝読中。前回は内積でした。内積（スカラー積）あれば、外積（ベクトル積）あり。今回は、Maximaにおけるベクトル表記のList流とMatrix流の２流派それぞれについて、外積の計算を行ってみたいと思います。外積はちょっとメンドイ？
※「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- wxMaxima 22.04.0
- Maxima 5.46.0(x86_64-w64-mingw32)
- SBCL 2.2.2 (SBCL = Steel Bank Common Lisp )
※Maxima を使った物理数学基礎演習ノート は以下のバージョンをダウンロードさせていただきました。
令和4 年3 月 第八回改訂
外積（ベクトル積）
前回の内積はベクトルとベクトルを掛けたのに結果はスカラーでお楽。しかし、高校（中学？）で習ったとおり、今回の外積はベクトルとベクトルを掛けたらばベクトルです。
\( \overrightarrow A \times \overrightarrow B \)
外積の場合「演算子」として「ｘ」印を使うことが普通かと。
さて前回も参照しております以下の過去回では外積あつかってます。
忘却の微分方程式(30) ベクトル解析その１、MathematicaとMaxima
そこで見たのは、『Mathematicaは、ESCキーを使った特殊シンボル入力機能をつかって外積をあらわす「×」印（cross)を入力可能である。二つのベクトルを「×」印で結んでやれば即、外積が求まる』ということでした。お楽。
しかし、調べてみたところでは、我らがMaxima様にはそのような「演算子」は無い模様です。上記の過去回では、「中川義行先生 Maxima 入門ノート 1.2.1」の「かっこいい」外積定義を参照したりしていました。なお、過去回で参照させていただいていたURLには「入門ノート」見つかりませなんだ。上記のリンクは神戸大様のサイトです。
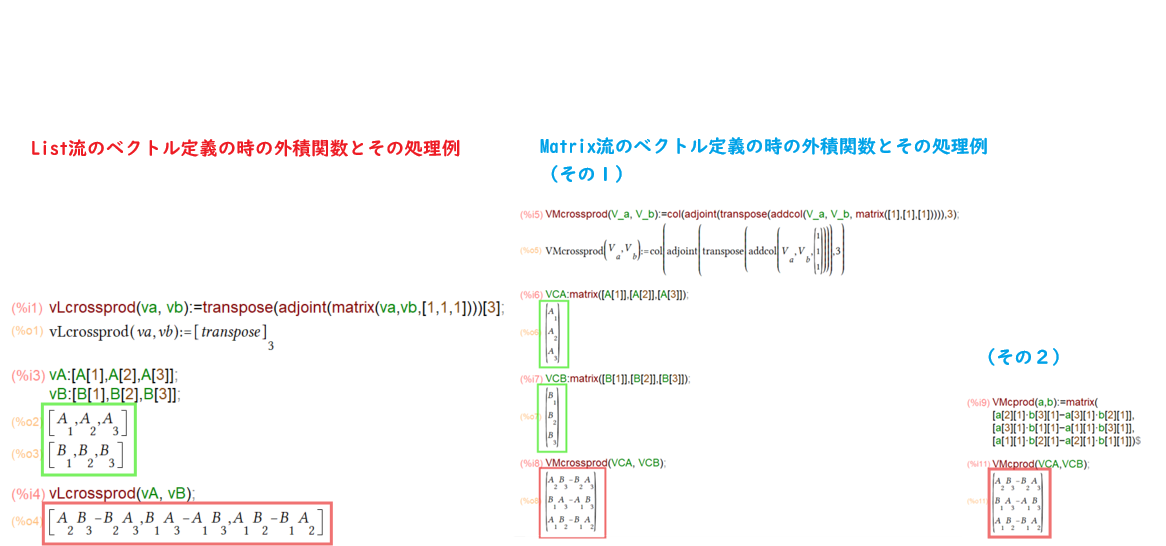
今回「演習ノート」P.79の、「4.1.3 ベクトルの外積（ベクトル積）」を見たらば、「演習ノート」も「入門ノートの外積定義」を参照されてました。ただし、「入門ノート」は基本List流でベクトル定義です。
結局、Maxima上で、以下３通りの外積計算用の関数が並び立つことに相成りました。
-
- 「入門ノート」スタイルの関数、List流派
- 「演習ノート」スタイルのその１（「入門ノート」を踏まえた定義）、Matrix流派
- 「演習ノート」スタイルのその２（シンプルな成分毎計算）、Matrix流派
Maximaでの表記が以下に。まずはList流派の入門ノート」スタイル
vLcrossprod(va, vb):=transpose(adjoint(matrix(va,vb,[1,1,1])))[3];
つづいて上記をMatrix流に改めた「演習ノート」スタイル
VMcrossprod(V_a, V_b):=col(adjoint(transpose(addcol(V_a, V_b, matrix([1],[1],[1])))),3);
最後に成分毎計算のシンプルMatrix流
VMcprod(a,b):=matrix([a[2][1]*b[3][1]-a[3][1]*b[2][1]],[a[3][1]*b[1][1]-a[1][1]*b[3][1]],[a[1][1]*b[2][1]-a[2][1]*b[1][1]]);
なお、こちらでのローカルルールとして、以下のように表記することにいたしましたですじゃ。
-
- 小文字のvで始まるのはList流のベクトル変数やベクトルを返す関数
- 大文字のVで始まるのはMatrix流のベクトルやベクトルを返す関数
まぜるとごっちゃになりそうだが、混ぜなければ大丈夫か？怪しい。
計算確認
上記を実際に計算して確認していきます。まずはList流から。
緑枠の２つのベクトル（List流）から、赤枠の外積ベクトル（List流）が求まってますな。
つづいて、Matrix流のその１から。
これまた同様。
最後にシンプル定義のMatrix流のその２。
当然、どれも結果は同じ。