溝口純敏様著「Maxima を使った物理数学基礎演習ノート」（以下「演習ノート」と略）を拝読中。前回は行列式でしたが、過去回ですこし練習してたので手抜きでした。今回は逆行列です。これまた過去回で練習済。でもいつも手抜きも何なので、今回は演習ノートにそって真面目に実習実施。ホントか？
※「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- wxMaxima 22.04.0
- Maxima 5.46.0(x86_64-w64-mingw32)
- SBCL 2.2.2 (SBCL = Steel Bank Common Lisp )
※Maxima を使った物理数学基礎演習ノート は以下のバージョンをダウンロードさせていただきました。
令和4 年3 月 第八回改訂
今回は「演習ノート」では、「4.2 行列とテンソル」の「4.2.4 逆行列関連」デス。
過去回での逆行列
以下の過去回で逆行列を練習してます。
忘却の微分方程式(35) 行列と線形代数への入り口、MathematicaとMaxima
上記では、ゴージャス？にMathematicaとMaxima比べてますが、今回はMaxima様に集中であります。
まずは逆行列
まずは逆行列デス。Aを行列とすると教科書的には以下のような記号で書くのが普通でないかと。
\( A^{-1} \)
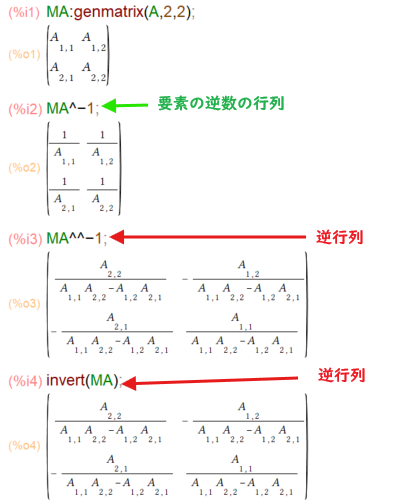
しかしながら、Maxima上で、行列Aの「マイナス一乗」を「^」記号で「^-1」のように書いてしまうと、行列の各要素の「マイナス一乗（つまりは逆数）」をとった行列になってしまいます。Maximaで逆行列を意味する場合は
^^-1
のように「サーカムフレックス（キャレット、ハットとも）」記号を２つ続けて記すようです。明示的な関数 invert() を使ってもよろし。操作はこんな感じ。
MA:genmatrix(A,2,2); MA^-1 MA^^-1 invert(MA)
実際にMaxima上で実行した例が以下に。
「演習ノート」はinvert()関数がお好みみたい。当方では、ことさらに ^^ してみました。
逆行列の性質いろいろ
さて、行列の逆行列に元の行列を右から掛けたならば、元の行列にその逆行列を右からかけたものと等価にして、その結果は単位行列となるっと。こんな感じ。
\( A^{-1} \cdot A = A \cdot A^{-1} = I \)
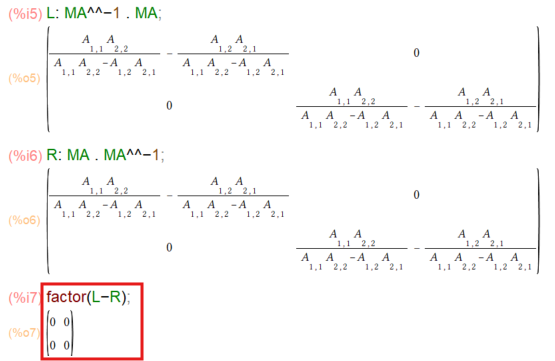
実際に行列MAを例にして上記の左半分の関係を確認する方法が以下に。
L: MA^^-1 . MA R: MA . MA^^-1 factor(L-R)
実際に計算したところが以下に。
お次は、行列の逆行列のそのまた逆行列は元の行列だと。こんな感じ。
\( ( A^{-1} )^{-1} = A \)
実際に行列MAを例にして上記の関係を確認する方法が以下に。
L2: (MA^^-1)^^-1 factor(L2-MA)
実際に計算したところが以下に。
今度は、『行列の逆行列を転置して逆行列とったら元の行列の転置だと』、こんな感じ。
\( (( A^{-1} )^T )^{-1} = A^T \)
実際に行列MAを例にして上記の関係を確認する方法が以下に。
L3: (transpose( MA^^-1 ))^^-1 R3: transpose(MA) factor(L3-R3)
実際に計算したところが以下に。
調子にのって、『行列の転置の逆行列を転置したら、元の行列の逆行列だと』、こんな感じ。
\( (( A^T )^{-1} )^T = A^{-1} \)
実際に行列MAを例にして上記の関係を確認する方法が以下に。
L4: transpose(transpose(MA)^^-1) R4: MA^^-1 factor(L4-R4)
実際に計算したところが以下に。
最後は、『行列の転置の逆行列は、元の行列の逆行列の転置と同じだと』、こんな感じ。
\( ( A^T )^{-1} = (A^{-1})^T \)
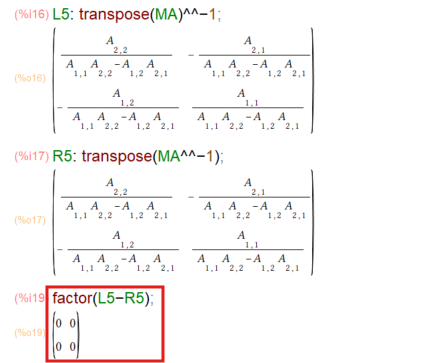
実際に行列MAを例にして上記の関係を確認する方法が以下に。
L5: transpose(MA)^^-1 R5: transpose(MA^^-1) factor(L5-R5)
実際に計算したところが以下に。
まあ、一通りの関係は計算できたみたい。そんなもんかい？