溝口純敏様著「Maxima を使った物理数学基礎演習ノート」（以下「演習ノート」と略）を拝読中。前回は逆行列でした。そのせい？か今回は連立一次方程式です。中学校以来お馴染みのやつ。ただね「演習ノート」では、行列のお勉強の一環ということで意義はあるけど実用的でない方法みたいデス。別途実用的なヤツを練習しとくと。
※「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- wxMaxima 22.04.0
- Maxima 5.46.0(x86_64-w64-mingw32)
- SBCL 2.2.2 (SBCL = Steel Bank Common Lisp )
※Maxima を使った物理数学基礎演習ノート は以下のバージョンをダウンロードさせていただきました。
令和4 年3 月 第八回改訂
今回「演習ノート」を学ばせていただくのは、「4.2 行列とテンソル」の「4.2.5 連立一次方程式(逆行列)」および「4.2.6 連立一次方程式(行列式)」あたりデス。
連立一次方程式
過去回でも連立一次方程式は使った記憶があるのだけれど、面と向かってやったというほどでもないみたい。そこで、今回は珍しく wxMaxima様のGUIをフルに駆使して、「演習ノート」の以下の例題を解いてみたいと思います。
2y + x = 3
5y + 4x = 6
連立一次方程式を解くのはプルダウンメニューから以下の項目を選択です。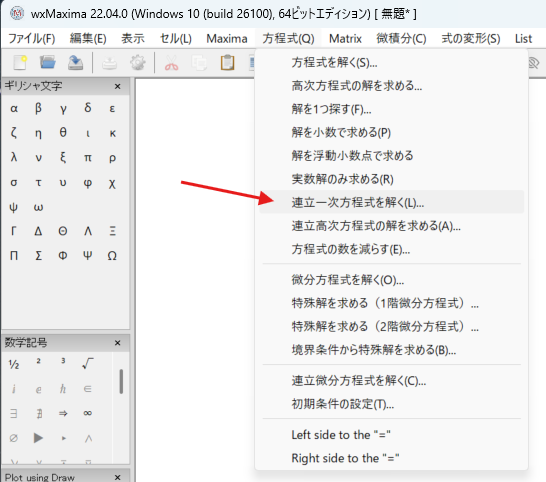
選択すると、何本の式が連立しているんだか聞かれます。ここでは２本っす。こんな感じ。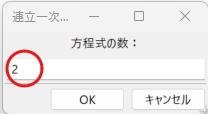
すると、実際に式を入力するように言われます。その際、値を求めるべき変数名をカンマ区切りで列挙して与える必要があります。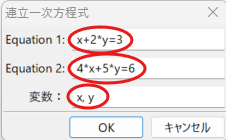
そしてOKっとボタンを押せば、解は一撃っす。
使われているのは linsolve関数ね。なお、linsolve関数は「ガウスの掃き出し法（老人もはるか太古の時代に習った気がしますが、忘却の彼方よな）」を使って求めてくれてるみたいです。
逆行列を使って求める、行列式を使って求める
しかし「演習ノート」では、linsolve関数つかってお茶を濁すようなことをせず、ちょうど練習したばかりの「逆行列」とか「行列式（クラメルの公式）」を使って連立方程式を解いてます。演習だからねえ。「演習ノート」に記載されているその方法を追いかけることはいたしませぬ。まあ、実用的にはやらんよな、ということであります。例によってGoogleの生成AI、Gemini 2.5 Flash様にその辺の事情をご説明いただきました。結論が以下に。
逆行列を使って求める方法について、詳しくは以下に。
計算量も多ければ、数値的にマズイケースもあるのね。ヤバイよ。
一方、行列式をつかってクラメルの公式適用する方法についてが以下に。
そういうことで、「実用的」には素直にlinsolveにお願いするのがよいみたい。ホントか？