
溝口純敏様著「Maxima を使った物理数学基礎演習ノート」(以下「演習ノート」と略)を拝読中。このところ基礎的な行列処理のお勉強が続いていました。前回は連立一次方程式でした。今回は一気に物理より?な課題に振れてます。物理からみると「線形な2自由度系の自由振動」デス。数学からみたら固有値問題らしいです。ムツカシそう。
※「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- wxMaxima 22.04.0
- Maxima 5.46.0(x86_64-w64-mingw32)
- SBCL 2.2.2 (SBCL = Steel Bank Common Lisp )
※Maxima を使った物理数学基礎演習ノート は以下のバージョンをダウンロードさせていただきました。
令和4 年3 月 第八回改訂
今回「演習ノート」を学ばせていただくのは、「4.2 行列とテンソル」の「4.2.7 固有値問題」あたりデス。
固有値問題
「演習ノート」には質点2個をバネ3個で接続した図が描かれているので物理の問題としては分かりやすいのです。しかし、タイトルに「4.2.7 固有値問題」と書かれているわりには、Maxima様のeigenvalues関数、eigenvectors関数などは一切登場しません。なお、過去回ではeigenvalues、eigenvectorsの練習もしています。
忘却の微分方程式(48) 反復練習12、固有値と固有ベクトル、対角化 Maxima
「みんな大好き P-1AP 」が活躍するの回っす。一方「演習ノート」の今回対象部分は、いままで練習の行列関係のMaxima関数を駆使しての「平手戦」です(正直、かなりメンドイです。)
今回は物理的な意味を「さらっと」味わうために、例によってGoogleの生成AI、Gemini様に以下のようなお伺い(プロンプト)をたててみましたぞ(楽な方に逃げたな自分。)
x 軸上を運動する質量M1およびM2の位置をx1(t)、x2(t)とする。左壁に固定されたバネ定数K1のバネがM1に接続されており、右壁に固定されたバネ定数K1のバネがM2に接続されている。さらにM1とM2の間にバネ定数K2のバネが接続されているとき、2質点が反対方向に動く場合と同方向に動く場合の条件を固有値を使って説明してください。
上記のようなボーバクとした問いかけにたいしても、以下のような明確なご説明をいただきましたぞ。
なんか、上記の方針だけで、素人老人はもう分かってしまったような気がいたします。早とちりだけれども。
今回は「外力なし」「減衰なし」という条件なので、運動方程式は以下のようにシンプルっす。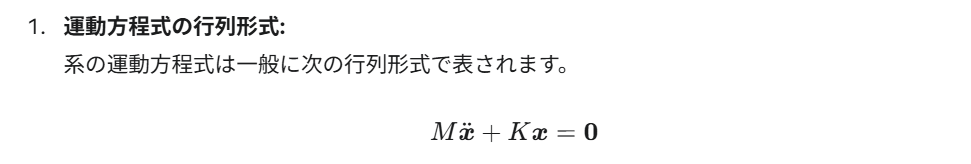
ここで、位置ベクトル x はこんなんデス。
\( \boldsymbol{x} = \begin{pmatrix} x_1 \ x_2 \end{pmatrix} \)
さらに、MとKは以下のようです。なお、質点M1も質点M2も同じ質量Mを持つということになってるみたい。
ここで以下の調和振動解を仮定して
\( \boldsymbol{x}(t) = \boldsymbol{\phi} e^{i\omega t} \)
固有値問題を立てると
\( \left( K – \omega^2 M \right) \boldsymbol{\phi} = \boldsymbol{0} \)
上記のようになるのだと。なおここで、固有値は、
\( \omega^2 \)
固有ベクトルは
\( \boldsymbol{\phi} = \begin{pmatrix} \phi_1 \ \phi_2 \end{pmatrix} \)
であります。
これをGemini様に解いていただくと、以下のようになりました(途中まで。)
そして上記の解は、2つの「モード」からなるみたいです。まず最初は質点が同方向に動くモード。
この対称モードでの固有ベクトルの比は以下に。当然その比は正。
\( \boldsymbol{\phi}_1 = \begin{pmatrix} 1 \ 1 \end{pmatrix} \)
その時の固有値(固有振動数の二乗)は、K1とMを使って以下のようであるみたい。
一方、質点が反対方向に動く「非対称」モードの固有ベクトルは以下です(比は負ね。)
\( \boldsymbol{\phi}_2 = \begin{pmatrix} 1 \ -1 \end{pmatrix} \)
その時の固有振動数は、K1、K2とMを使って以下のようであるみたい。
ううむ、何でもお見通しのGemini様にオンブにダッコですわい。まとめが以下に。
まあ、お楽だし、いいか。
