
前回まで続いたバナナ関数(Rosenbrock関数)の最適化デモ、今回から別の単元?に入ったのでお別れかと思いきや、ここでも登場。前回までは最適化に勾配計算が必要なoptim関数。しかし今回は微分(勾配情報)を使用せずに、多変数関数の局所的最小値を求めるfminsearch関数のご登場。もう一つのシンプレックス法だと?
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※Windows11上の Scilab2024.0.0を使用させていただいております。(Scilabについては御本家 Scilab 様へ)
前回までの「最適化」の単元?では、Rosenbrock関数(バナナ関数)を題材に Scilab所蔵のoptim関数により最適化(最小値を求める)をこれでもかとデモしてくれました。まあね、それだけRosenbrock関数が「最適化のデモ」に向いた「手ごろな難しさで分かりやすい」関数であったと。そして optim関数を適用するには基本「勾配」(微分)が計算できないとなりませぬ。解析的に求めた勾配関数だけでなく、前回は数値的に求めた勾配をつかっての optim関数のデモもありました。
これでいいじゃん!
と思ったらそうでもありませぬ。次の単元 fminsearch ではその名の通り、fminsearch関数の御登場なんであります。シンプレックス法?どこかで聞いた気がするんだが。。。
fminsearch_rosenbrock.sce
今回「鑑賞」させていただくScilabのデモは、fminsearch_rosenbrock.sceです。以下のデモ選択画面から起動できます。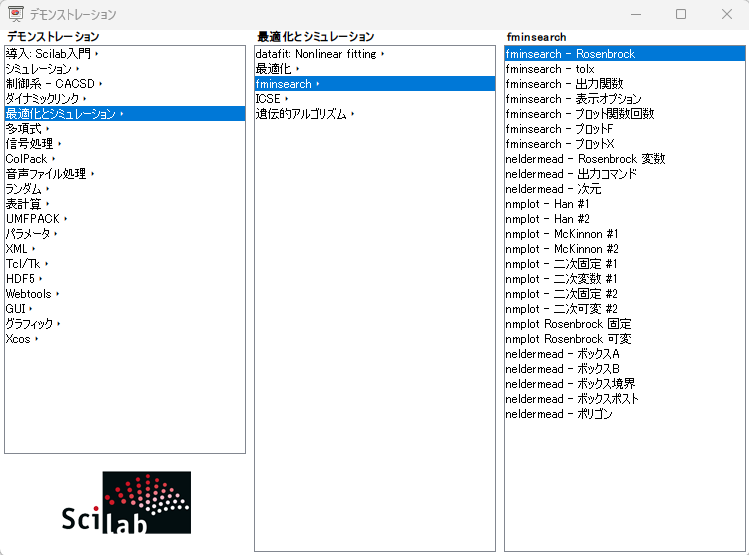
fminsearch関数に「捧げられた」単元みたいです。その冒頭に登場するのが、またもや Rosenbrock関数(バナナ関数)です。この関数は、前回までのoptim関数のように微分(勾配情報)をつかわず、多変数関数の局所的最小値を求めることができるみたい。アルゴリズムにネルダーミード法というものをつかっているそな。ネルダーミード法を調べるとその説明の中に、
シンプレックス法
というどこかで聞いたお名前が出てくるのです。お惚け老人は、ほぼ半世紀前、計算機実習でFORTRANを習っていた頃にお聞きしましたぞ。線形計画法とかリニア・プログラミングとかいう「なにやら恐ろし気な」世界に誘うものでした。しかしね、バナナ関数、線形じゃありません。バリバリの非線形っす。そう思ってちょいとGemini様に御伺いをたてると、こんなご回答を得ました。
ほほう、お惚け老人の記憶の奥底にある「シンプレックス法」とは幾何学的発想は根を同一にしているけれども、どうも異なる方法なのね。ホントか? ネルダーミード法は、非線形でもあるいは勾配が求まらないような「飛躍」があっても「なんとか」してくれることもあるみたい。まあ、駄目なときは万歳することもあるみたいだけれども。
Gemini様がお教えくださったネルダーミード法のおおまかなところが以下に。
「図形が変形」しながら谷底へ降りていく様子が、アメーバが移動する様子に見える(私は実際にプロットして見たわけではないが)ために「アメーバ法」とも言われるらしいっす。
デモを実行
「ご回答」部分に赤枠つけました。何度となくバナナ関数最適化のデモを見てきたので、忘却力の老人も解空間の座標(1.0,1.0)で関数値0が「目標」ということは覚えてしまいました。赤枠みると、fminsearch関数もそれなりに肉薄しているみたい。下の註釈みるとオプションの設定次第でどこまで追求するかは制御できると。今回のデフォルト設定でも85回も繰り返してる?結構大変。でも計算してくれているのはScilabなので知ったことではない? すみません、いつもお世話になっておりますのに。
