拝読中の溝口純敏様著「Maxima を使った物理数学基礎演習ノート」（以下「演習ノート」と略）の今回は「テンソルの不変量」です。ようやくテンソルの核心領域に肉薄？といって素人老人はなんもわかっちゃおりません。そういうときはGemini様に御伺いをたてれば「分かったような気」になれるんだこれが。大丈夫か？
※ 「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- wxMaxima 22.04.0
- Maxima 5.46.0(x86_64-w64-mingw32)
- SBCL 2.2.2 (SBCL = Steel Bank Common Lisp )
※Maxima を使った物理数学基礎演習ノート は以下のバージョンをダウンロードさせていただきました。
令和4 年3 月 第八回改訂
今回「演習ノート」を学ばせていただくのは、「4.2 行列とテンソル」の「4.2.11 テンソルの不変量」デス。
Tensor Invariant
さっそくGoogleの生成AI、Gemini様に「テンソルの不変量」についてお教えいただくとこんな感じ。
そういうものなのね、と「あいわかった」つもり。
さて、「よく登場する」２階のテンソルの場合、テンソルの不変量は以下のごとくに求まるみたいです。
おお、二階のテンソルの「基本不変量」は第１、第２、第３と呼ばれているのね。その意義が以下に。
そゆこと。分かったような、分からぬような。まあ、お惚け老人のような凡人は実例を数こなさないと分からぬわな、 分かるのか、ホントに？
演習ノートでの第１、第２、第３不変量
演習ノートでは、以下の対角行列Mについて、その行列式を解いて３次方程式をもとめ、その係数を導出してくださってます。
\(
M =
\begin{pmatrix}
σ_1 & 0 & 0 \\
0 & σ_2 & 0 \\
0 & 0 & σ_3 \\
\end{pmatrix}
\)
\( 第一不変量（トレース） = σ_1 + σ_2 + σ_3\)
\( 第二不変量 = σ_1 σ_2 + σ_2 σ_3 + σ_3 σ_1\)
\( 第三不変量（行列式） = σ_1 σ_2 σ_3\)
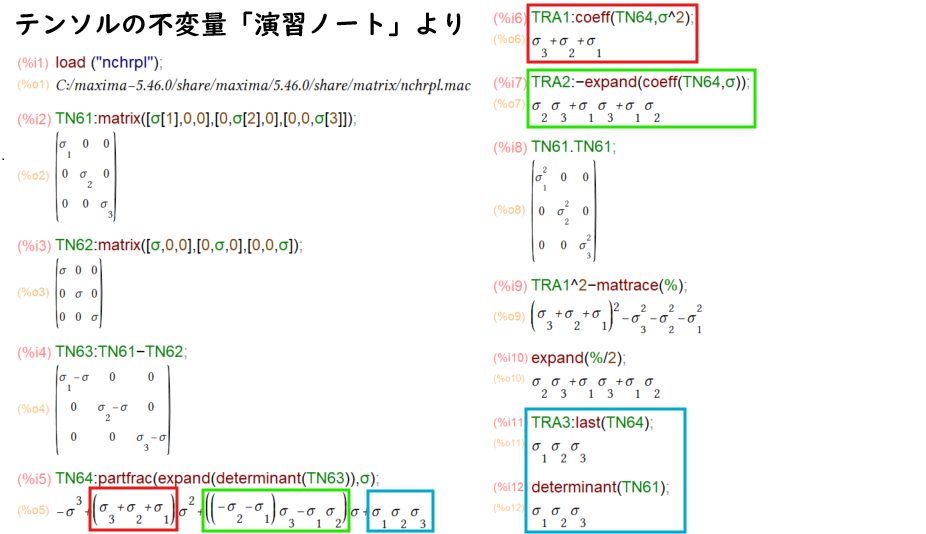
Maximaさまにお願いして、演習ノートの足跡をたどりましたものが以下に。なお nchrplは mattrace、ncharpoly関数が定義されているパッケージです。過去回で調べたところでは「泣く子も黙るMACSYMA様」のCHARPOLYという関数と同等のもの（ncharpoly)をMaxima上でも欲しいということで設けられたパッケージみたいデス。
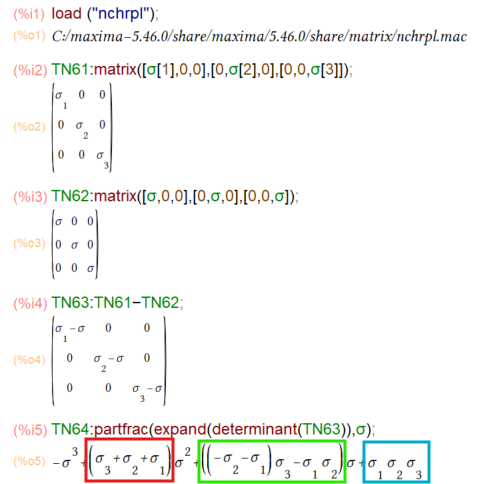上記のTN64で、３次方程式が求まりました。そこで２次の項の係数（赤枠）、１次の項の係数（緑枠）、定数項（青枠）を取り出せば、第１、第２、第３不変量であると。
これだけではサッパリよな。後で物理の実例にあたって、シミジミ不変量の有難みを噛みしめないと。ホントか？