
「浜の真砂は尽きるとも世にバナナ関数(Rosenbrock関数)の種は尽きまじ」、ホントか? 遥かな過去からバナナ関数ばかり練習しているような気がしてます。当然、今回もです。前回につづき「もう一つのシンプレックス法(ネルダーミード法)」を駆使するfminsearch関数使ってです。今回はその精度を出し入れ?
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※Windows11上の Scilab2024.0.0を使用させていただいております。(Scilabについては御本家 Scilab 様へ)
fminsearch_tolx.sce
今回「鑑賞」させていただくScilabのデモは、fminsearch_tolx.sce です。以下のデモ選択画面から起動できます。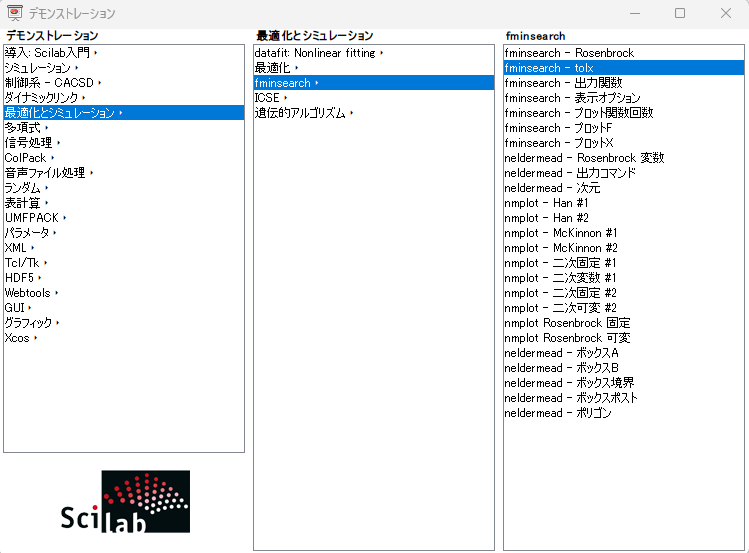
最適化のターゲットは、モチのロンで、バナナ関数(Rosenbrock関数)です。そして最適化(最小値を求める)のは、前回同様のfminsearch関数(ネルダーミード法)を使用です。では、何がデモのテーマかといえば
オプション
です。Scilabのfminsearch関数のHelpファイル的には、options.TolXなるパラメータの操作です。「シンプレックス(単体)」サイズの絶対誤差みたいです。前回は何も指定しなかったのでデフォルトの 1e-4が使われておったと。今回のコードをみやればこんな感じ。
前回の値の「100倍」デカイ値を設定してます。手抜きだのうワレ。それでもま、0.01だけれども。
デモ結果
赤枠内の「最適化結果(最小値)」をみると、前回の結果より悪化しとりますなあ。それなり? まあ、手を抜いたのだから当然か。緑枠のTolX値は設定の通り。黄色枠の繰り返し回数は70回、100倍手抜き?で、前回の85回より15回短縮できたと。そんなもんかい?どんなもんだい?微妙?
