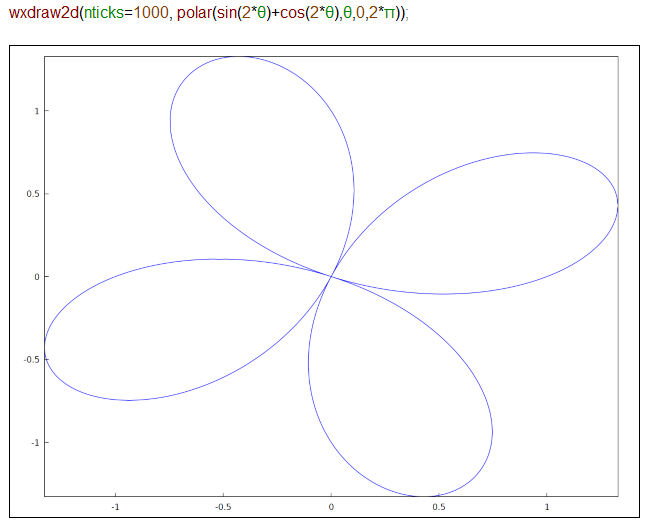
Mathematicaのチュートリアルを読みながら、同じことをMathematicaとMaximaでやってみております今回は極座標であります。例によって「よきにはからって」くれるMathematicaに対し、ちゃんと指定しないと思ったように動いてくれないMaximaの性格?の違いが現れております。Maximaを深く分かっている人にはどうということないのでしょうが。
※「忘却の微分方程式」投稿順 index はこちら
参照させていただいておりますWolfram社のドキュメントは以下です(いつもながら学生でもないのに使わせていただいてます。)
今回は、「先攻」Mathematicaということで行きたいと思います。
極座標によるプロット
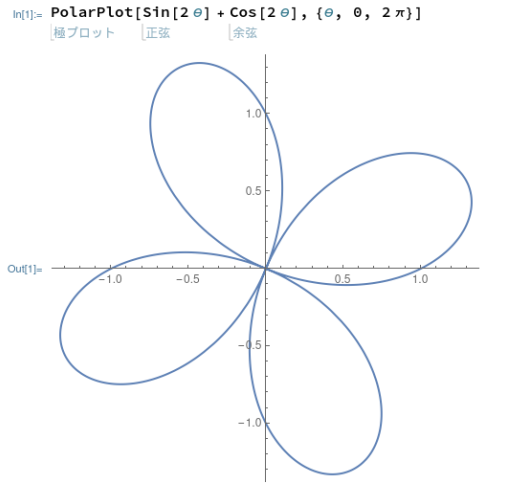
Mathematicaの場合、極座標で記述された関数をプロットする専用の関数がありました。それを使えば、上記のページの例題関数など、特に何か細かい指定をすることなく綺麗にプロットすることが可能でした。
 Maximaで極座標を使ってプロットをしようとする場合、「大域変数plot_optionsのtransform_xyに座標変換を行う関数(polar_to_xy)を指定する」といった方法もあるようでした。今回使用してみたのは、グラフィックオブジェクト polar を使用する方法です。日本語マニュアルへのリンクはこちら。
Maximaで極座標を使ってプロットをしようとする場合、「大域変数plot_optionsのtransform_xyに座標変換を行う関数(polar_to_xy)を指定する」といった方法もあるようでした。今回使用してみたのは、グラフィックオブジェクト polar を使用する方法です。日本語マニュアルへのリンクはこちら。
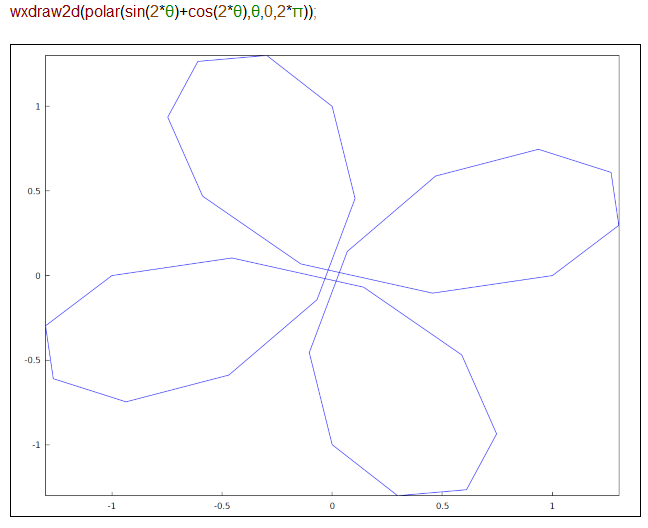
早速 wxMaxima(Maximaに被せたGUIの処理系)でやってみると、こんな感じ。ガタガタすぎるんでないかい!
 まあこの対処方法は、私のような素人でも分かります。nticks値をデカくしてやったら良いのであろうと。適当、ありがちに1000としてみました。こんな感じ。
まあこの対処方法は、私のような素人でも分かります。nticks値をデカくしてやったら良いのであろうと。適当、ありがちに1000としてみました。こんな感じ。
ガタガタ感はなくなりましたな。しかし、本当は、Mathematica風にX軸Y軸の表示など変更したかったのです。しかし、調べてもよく分からず、断念してしまいました。
さらにMaximaで困ったのがMathematicaの以下の機能です。X, Y軸でなく、Θ軸というべきか、を表示することができます。
 Maximaではそういう軸オプションは見当たらず。無理やりやろうと思えば円を描いて所定の位置に小さい線分を置いていったら、似たような「図形」は描けるだろう、とは思うのです。まあ、そこまでやる元気が無いです。
Maximaではそういう軸オプションは見当たらず。無理やりやろうと思えば円を描いて所定の位置に小さい線分を置いていったら、似たような「図形」は描けるだろう、とは思うのです。まあ、そこまでやる元気が無いです。
極座標への変換
全然凄い機能ではないのですが、Mathematicaは「痒い所に手が届く」感じで、直交座標から極座標への変換関数が存在します。こんな感じ。
Maximaで直ぐに使える似たような関数無いかと探してみましたが、ちょっと見当たりません。このくらい、自分で定義した方が早くね、ということで定義してみました。こんな感じ。
前回の三角関数では登場しなかった、atan2にお出ましいただけば、ほぼほぼ問題解決。歴史と伝統のatan2(古の時代のFortranコンパイラが起源で、多くの処理系にひろまった、と聞いております。実際、私が1970年代に「計算機実習」やったときにもatan2ありましたぜ)、やっぱ頼りになります。
微分方程式にたどり着くまで、まだまだ先は長いな。。。