前回は極座標でしたが、今回は対数関数、Logです。改めて使わせていただいてみると、Mathematica、Maximaともにクセがあり、似ているようで似ていない感じもチラホラと。まあ実用的に一番お世話になっているのは対数グラフくらいですかね。あんまり数学という感じでもない。
※「忘却の微分方程式」投稿順 index はこちら
Wolfram社Mathematicaのチュートリアルを読みながら、同じことをMathematicaとMaximaでやってみております。今回学生でもないのに参照させていただきましたのは、以下です。
チュートリアルのタイトルには、指数と対数とありますが、チュートリアルで使ってみているのはLog関数ばかりに見えます。当然、その入力に指数関数は登場するのでありますが。
対数関数のエクササイズ
今回の「先攻」はMaximaとさせていただきました。自然対数の底(ネイピア数） e は、％を使った記法で、%e で入力できました。Maximaが既定で持っている対数関数 log () は自然対数のみのようです。log(2)などとしても勝手に浮動小数の近似値が出力されることはなく、近似値が欲しければfloat()関数に渡す必要があるようです。また、常用対数が欲しければ、自分で定義するしかないみたいです。以下では常用対数の場合、近似値で答えがでるようにしとります。
続いてMathematicaの場合です。Mathematicaは「大文字で始まったら既定の関数とか変数」であるようなので、自然対数の底 e は 大文字のE一文字でOKです。鳴れないとちょっと変。また対数関数は Log[] と、例によって大文字で始まり、角カッコです。
Maxima同様、Log[2]などとしても直ぐに近似値を出力することはありません。Mathematicaの場合は、N[]関数に渡すことで近似値にして返してくれます。Maximaと異なり、自然対数の底以外もLog[]関数で扱うことができます。第１引数に底を与えれば、特に自分で関数定義することなく、常用対数も計算できます。
高校（中学だっけか？）で対数関数をやったときに、最初の方でやった気がする対数関数の展開（掛け算や割り算が足し算、引き算になるやつ）や、縮約（その逆）については、Maximaは直ぐにできたのですが、Mathematicaの場合、既定の関数が見当たりませんでした。自分で書けということなのか、もっと調べたら何かよいものが出てくるのか、今のところ不明。
以下はMaximaでの展開、縮約の例です。
対数グラフ
数学というより、エンジニアリングユースで一番お世話になるのが対数グラフですね。グラフを描くソフトウエアのほとんどが、なんらかの形で対数グラフをサポートしていると思います。MaximaとMathematicaも例外ではありません。
Maximaの片対数グラフ
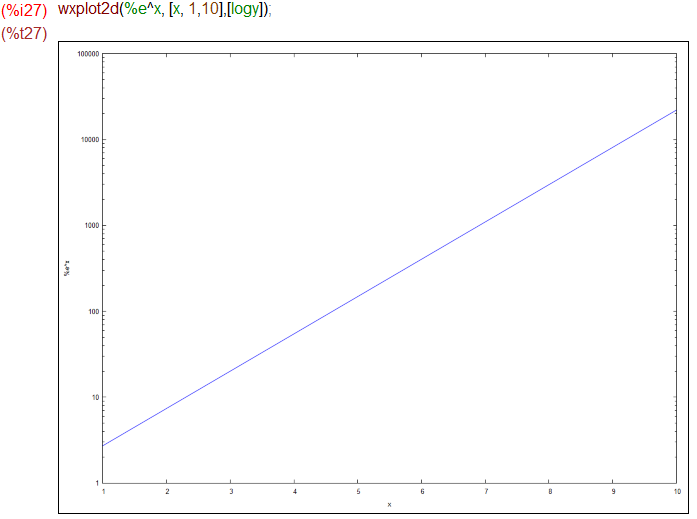
Maximaの場合、普通にプロットするつもりで、オプションのlogyをtrueにすればY軸を対数目盛にしてくれます。こんな感じ。
Maximaの両対数グラフ
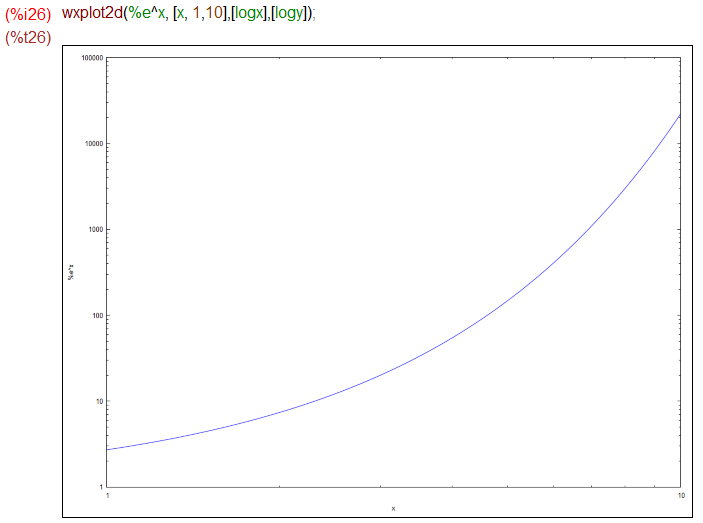
両対数にするにはlogyに加えて、logxもtrueとします。こんな感じ。
Mathematicaの片対数グラフ
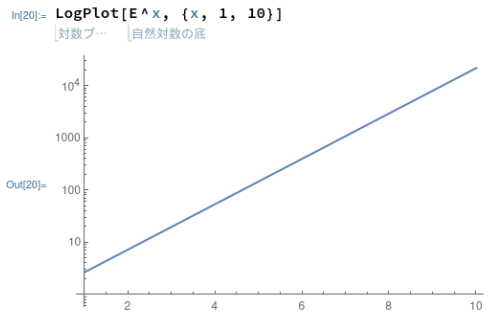
Mathematicaの場合、片対数専用のプロット関数があるので、それを呼び出せば片対数グラフが得られます。
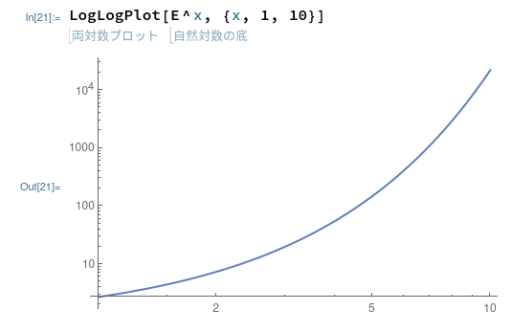
当然、両対数グラフには両対数グラフ専用の関数が用意されています。覚えやすいネーミングといえば覚えやすい。
まあ、さらっと撫でただけですが、こんなもんで何とかなるかね。なにかあったらまた調べれば良いし、と。いいかげんだな。