通り一遍舐めていってもMaximaもMathematicaも上手くならないので、ちょっと方針を変更しました。反復練習あるのみ、と。しかし、忘却力のこの年寄りが反復練習してもザル、結局、ファイルに残したものだけが「記憶(ストレージ)」に残ると(計算機におまかせ。)反復練習には大学初年級くらいのところから始めたいです。最初は線形代数とな。
※「忘却の微分方程式」投稿順 index はこちら
反復練習(といっても反復してくれるのは計算機であって私ではなく、記憶するのも私ではないです。私の実存が疑われる今日この頃)の課題として、以下の「参考書」を使わせていただくことにしました。
リンク先が改訂9なので上記は改訂9といたしましたが、私が所持しておるのは「改訂1」です。大分古いです。現在すでに改訂9ということなので、力の入りかた凄まじい限りです。私の所持している版には表紙に「単位なんて楽に取れる!」とか煽り文句が並びます。多分大学の初年級あたりで線形代数の授業あり、最初は簡単なのに、少しすると急に「分からん」と困った学生さんがご購入になるのでしょうか?読んで面白く、分かったような気に直ぐになれる本だと思います(個人の感想です。)分かった気になったら自分で演習やって定着しないと。
今回の課題
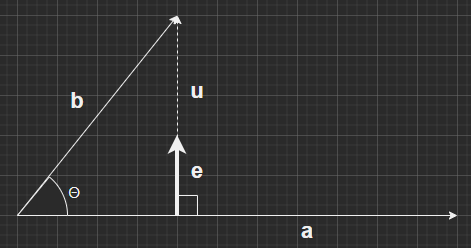
今回の課題を冒頭のアイキャッチ画像に掲げました。ベクトルaとベクトルbがあり、ベクトルbのベクトルaへの正射影が計算できると。するとベクトルaに垂直なベクトルuを求めることができるからさ、その単位ベクトルeの成分を求めよ、という感じでしょうか。
Maximaで書いたお答え
こんなんでどうでしょ。途中経過も求まるし。上記御本ではベクトルは列ベクトルなのです。しかし列ベクトルの入力メンドイということでリストをそのままベクトルとみなして計算する方式です。なお、どこにも2次元とか3次元とか登場しないので、多分、n次元のベクトルで計算できる筈。ホントか?
/* ベクトル vA に垂直な単位ベクトル vE を求める */ norm(x):=sqrt(x . x); getvU(vA, vB):=vB-((vA.vB)/(vA.vA))*vA; getvE(vU):=vU/norm(vU);
Maximaへのロード
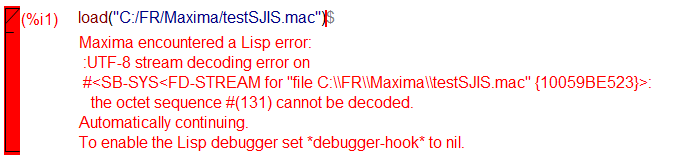
上記ソースを test.mac という名でセーブしてMaximaにロードすれば必要な関数が定義されます。しかし一点注意があります。GUIありの、wxMaxima 21.05.2 を使っておりますが、文字コードがUTF-8でないと以下のようなエラーに遭遇します。
WindowsPC上のエディタでテキトーに書いたらSJISになっていて、ロードしようとしたら以下のようなエラーに遭遇しました。
ちゃんとUTF-8でセーブしなおせば、OKです。
なお、ロードした関数名リストを確認するとこんな感じ。
演習問題1
ちゃんと、自分の頭で解いて理解せよ、という趣旨の筈の演習問題をMaxima様にお願いして解いてしまいます。後ろ暗い?先のある学生様ではないので許してくだされ。計算機だけが頼りの年寄りです。
ま、当然ですが、解答は合っておるみたい。ただし、本来垂直な単位ベクトルは上向き、下向き?の2方向ありえるので、プラスマイナスであるべきなのでしょう。しかし、上記で計算しているのは一方のみであります。
実践問題1
恐れ多いことに実践問題もほれこの通り。
解けます(私じゃなく、Maxima様が。)