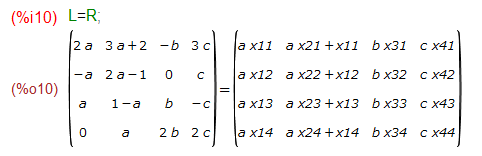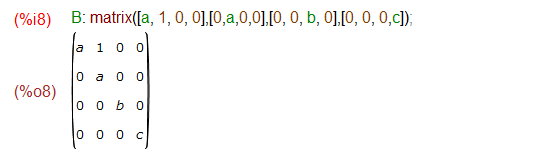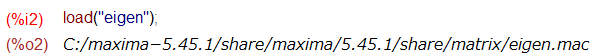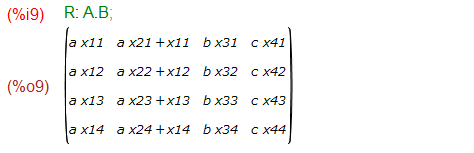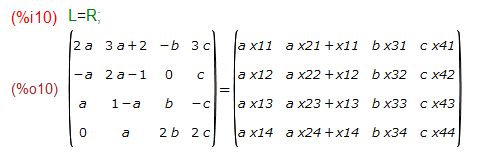今回は行列を列ベクトルとして分割です。しかし列ベクトルと言われて引っ掛かりました。今までのところリストをそのまま行ベクトルとしてみなして処理をしてきています。Maximaで列ベクトルにするのはどうしたら良いの?調べてみたらモジュールのロードが必要でした。eigenとな。もろ線形代数っぽい?
※「忘却の微分方程式」投稿順 index はこちら
以下の参考書(以下URLは「改訂9」)の、以前の「改訂1」版の演習問題をMaximaの練習用に使わせていただいております。
今回は演習問題5「行列の列ベクトルへの分割と変形」です。
問題の左辺の行列定義
左辺は普通にリスト(行ベクトル)を並べて行列を定義してみます。
L: matrix([2*a, 3*a+2, -b, 3*c],[-a, 2*a-1, 0, c],[a, -a+1, b, -c],[0, a, 2*b, 2*c]);
定義したところがこちら。4x4の行列ができました。
問題の右辺の行列定義
右辺は、求めるべき行列Aともう一つの行列、ここではBと勝手に名付けました、の行列積です。Bは左辺同様に普通にリストで定義してしまいます。こんな感じ。
B: matrix([a, 1, 0, 0],[0,a,0,0],[0, 0, b, 0],[0, 0, 0,c]);
Maxima上では、
一方、問題の4x4の行列Aは、問題にそって4個の列ベクトルを並べて作ってみています。Maxima上ではあまり意味ないケド。列ベクトルは eigen パッケージをロードしないと使えないようなのでロードしてみました。
上記をロード後、列ベクトルの定義ができるようになるので、以下のようにAを定義してみました。問題では、列ベクトルは最初から数値で与えているのですが(見れば分かるので)、ここではとりあえず未知数扱いでやってみます。列ベクトルの1個目だけは表示しましたが、長くなるので他は中身を見せていません。
まあ、これで列ベクトルからAができました。行列の右辺は、AとBの行列の掛け算なので、以下のようになります。
未知数の決定
問題では、最初から数値で与えてますが殊更に左辺=右辺とするとこんな感じ。
要素毎に16元の連立方程式にしてx11~x44を決定すれば機械的に解けますが、メンドイ。問題文どうよう確かに見れば答えが分かってしまう。。。左上隅だけをsolveしてみればこんな感じ。
結局、暗算?(単に値を比べるだけ)で値を設定できると。
再度行列Aを定義しなおし、そして問題の転置行列 tA を求めてみると以下のとおり。
まあ、これでAと転置行列Aが求まったけれども、手でやった方が早い?でもま、ちょっと係数複雑になったら、「多分確実に」間違えるから、自分。