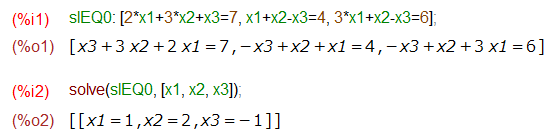連立一次方程式に入るために関係するmaximaの関数を調べて置こうと思います。教科書見ると「クラメルの公式」使ってとか「掃出し法」つかってとかいろいろありますが、Maximaの場合solve一発で解けてしまいます。解く前にRankとか確認して、解けるんだか解けないんだか当たっておく感じ?
※「忘却の微分方程式」投稿順 index はこちら
※数学の勉強のための以下の参考書(以下URLは「改訂9」)の「改訂1」版の演習問題をMaximaの練習用に使わせていただいております。
例題を使わせていただいとりますが、数学の勉強には全然なってないです。すみません。
また今回書いた後で、足立健朗様の以下のPDFが大変ありがたいものであることに気づきました。先に(見つけて)読んでおけば楽だったです。
行列計算における数式処理ソフト maxima の利用について
連立一次方程式をとく
連立一次方程式方程式を解くだけであれば、以下のようにそれぞれの方程式をリストにし、未知数のリストと合わせて solve() に渡せば以下のように答え一発で求まります。らくちん。
連立一次方程式から係数行列、拡大係数行列をとりだす
上記の方程式としての記法でなく、係数行列を求める場合は coefmatrix()関数に方程式リストと未知数リストを与えれば求まりますな。さらに方程式が非同次の場合であれば、拡大係数行列は augcoefmatrixに方程式リストと未知数リストを与えれば取り出せると。
係数行列から逆行列を得るのは invert
上記で係数行列を取り出せれば、invert() で逆行列を求めるのも一撃。
係数行列、拡大係数行列のrank、階段行列を求める
係数行列、拡大係数行列を取り出してあれば、それを rank() に渡すことで行列の階数が求まります。
- 同次n元連立1次方程式であれば n – rank(係数行列)が>0ならば自明な解があり
- 非同次n元連立1次方程式であれば rank(係数行列)= rank(拡大係数行列)であれば解が存在する
と。私が言ったんじゃありません。教科書の受け売りです。知らんけど。
求めているところが以下に。ついでに階段行列がどんなんだかも分かりますです。
計算は楽。でも数学は身につかない。トホホ。