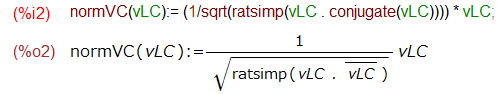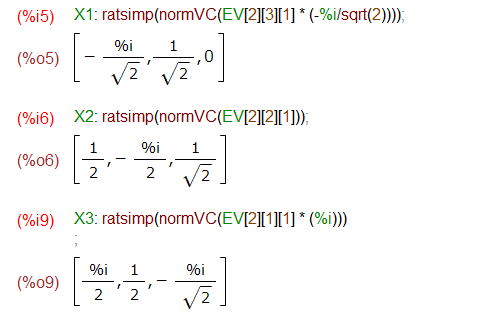前回、「エルミート行列をユニタリ行列を用いて対角化」をやってみました。実数の対称行列について過去やったのと手順はほぼ同じですが、エルミートと聞いただけで記憶が忘却の彼方に飛ぶ感じがします。今回はもう一度同じ手順を練習。行列は3x3にサイズアップ?大して変わらんけど。気持ちの問題。
※「忘却の微分方程式」投稿順 index はこちら
※以下の実習は、みんな大好き Maxima の以下のバージョン(Windows)で行なっております。
-
- wxMaxima 21.05.2
- Maxima 5.45.1 (wxMaximaの裏で動いているMaxima本体)
※以下の参考書の「改訂1」版の演習問題を題材に使わせていただいております。
今回復習する手順
今回復習する「エルミート行列をユニタリ行列を用いて対角化」する手順は以下です。サイズが前回の2x2行列から3x3行列になっているので正規化する固有ベクトルが2つから3つになっているのが主な違いです。
固有ベクトルに何やら定数を掛けているのは教科書の例題の途中経過と「ピタリと」表現合わせたいがための小細工です。また順番入れ替えているのも同じ。
Ah: matrix([0,%i,1],[-%i, 0, -%i], [1,%i,1]); normVC(vLC):= (1/sqrt(ratsimp(vLC . conjugate(vLC)))) * vLC; EV: eigenvectors(Ah) X1: ratsimp(normVC(EV[2][3][1] * (-%i/sqrt(2)))); X2: ratsimp(normVC(EV[2][2][1])) X3: ratsimp(normVC(EV[2][1][1] * (%i))) Ux: addcol(transpose(X1), transpose(X2), transpose(X3)) ratsimp(Ux^^-1 . Ah . Ux)
課題
今回は以下のエルミート行列 Ah をユニタリ行列を用いて対角化する、という問題です。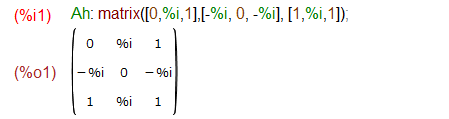
前回も使った複素ベクトルの正規化のための補助関数?を定義しておきます。
固有値、固有ベクトルからユニタリ行列を求める
一番メンドイ固有ベクトルを求めるところ、eigenvectors()一発です。Maxima様のお陰です。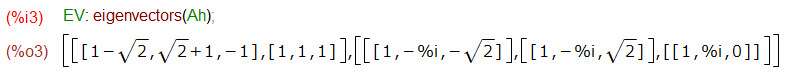
上記の結果の前半は固有値で、後半が固有ベクトルです。固有ベクトルを取り出した上で正規化しているところが以下に。定数かけたり、順序を入れ替えたり「許される」小細工しているのは前述のとおり。
列ベクトル化した上で結合してユニタリ行列を作る手順が以下に。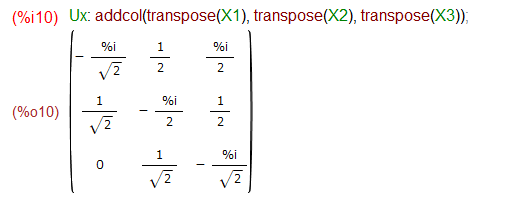
対角化
ユニタリ行列Uが求まれば、U-1 Ah U で対角化ができる、と。
できましたな(といって計算しているのはいつものとおりMaxima様ですが。)